Формы записи комплексного числа

В данной публикации рассмотрена тригонометрическая форма комплексного числа с интерпретацией на коордлинатной плоскости, формулами расчета аргумента и примером для лучшего понимания изложенного материала. Также представлена базовая информация по показательной форме данного типа числа.

Та
запись комплексного числа, которую мы
использовали до сих пор,
называется алгебраической
формой записи комплексного числа.
Часто бывает удобна немного другая
форма записи комплексного числа.
Пусть

и
φ = arg z.
Тогда по определению аргумента имеем:

Такая
форма называется тригонометрической
формой записи комплексного числа.
Как видно, для того, чтобы перейти от
алгебраической формы записи комплексного
числа к тригонометрической форме, нужно
найти его модуль и один из аргументов.

Пусть задано комплексное число $z=a+b i$ .
Как известно, его можно изобразить на комплексной плоскости точкой, абсцисса которой равна действительной части этого
числа, то есть $a$, а ордината – мнимой части
$b$ (рис. 1).

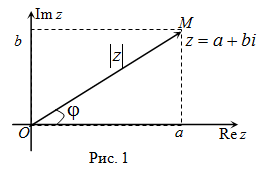
Таким образом, для всякого комплексного числа $z=a+b i$
справедливо равенство

которое называется тригонометрической формой комплексного числа $z$ .

Задание. Комплексное число
$z=-i$ представить в тригонометрической форме.

Решение. Для заданного числа действительная часть
$a=0$, а мнимая часть
$b=-1$ . Тогда
модуль этого числа

Отсюда получаем, что

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Урок по алгебре в 10 классе Учитель: Печенкина Евгения Евгеньевна

Домашнее задание: П.34(учить) №34.22 №34.1 №34.29(в) №34.30(в)

Рассмотрим координатную плоскость Комплексное число z = x + yi изображается на плоскости точкой z ( x , y ). Re Im 0 1 1 Z х у

Тригонометрическая форма записи комплексного числа

Re Im 0 1 1 Z Рассмотрим вектор с началом в точке О и концом в Z х у Опр: Длина = называется модулем (r) комплексного числа z ϕ – 1 Угол , образуемый вектором Z с положительной полуосью x, называется аргументом числа z ( Arg z)

Любое значение аргумента z определяется по формуле: = arg z + 2 k π Модуль числа z определяется по формуле: r =

Пример : Найти модуль комплексного числа x = 4; y = -3 r =

Re Im 0 1 1 Z х у cos s Комплексное число z = x + yi x=r cos z = x + yi =r (cos i sin ) Тригонометрическая форма записи комплексного числа

Задание№1.Найдите модуль и аргумент комплексного числа: 1) z = 4 + 4i; 2) z= 3 – 3i; 3) z = i

Задание №2. Представьте данное комплексное число: а) в алгебраической форме: z = 2 (cos π/4 + i sin π/4); z = 4 (cos π/3 + i sin π/3); б) в тригонометрической форме: z = 1 + i ; z = 2 + 2 i .

Правило №1. Умножение При умножении двух комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются.

Пример: Найти произведение этих чисел. Решение:

Правило №2: Деление При делении двух комплексных чисел, заданных в тригонометрической форме, их модули делятся, а аргументы вычитаются.

Пример: Найти частное этих чисел Решение:

Домашнее задание: П.34(учить) №34.30(г) №34.23 №34.32(а) №34.29(г)

Задание №1. Выполните действия

а ) 3 (cos + i sin )· (cos + i sin ); б ) (cos + i sin ): (cos + i sin ) Задание №1. Выполните действия

Ответы: а ) 6 (cos + i sin ); б ) (cos + i sin )

Задание №2. Запишите в тригонометрической форме комплексное число

а) -3 – 3 i ; б) −10 𝑖 ; в) 3 𝑖 ; г) Задание №2. Запишите в тригонометрической форме комплексное число

Ответы: а) б) в) 3 г)

Задание №3. Запишите в алгебраической форме комплексное число

Задание №3. Запишите в алгебраической форме комплексное число 𝑧 = 4 ( 𝑐𝑜𝑠 + 𝑖𝑠𝑖𝑛 )

Ответы: i * i

Задание №4. Изобразите на координатной плоскости комплексное число

Задание №4. Изобразите на координатной плоскости комплексное число 𝑧 = – i 𝑧 = 2 -3i

Ответы: Re Im 0 1 1 -1 Arg 𝑧 = 2 -3 Arg 𝑧 = arccos

очевидно можно представить как радиус-вектор:

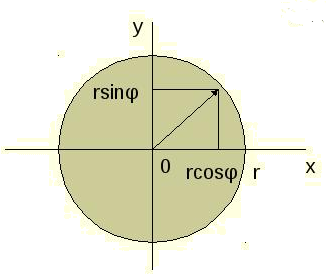
Получается, что модуль комплексного числа z будет равен 10.
В прошлой части я рассказал про две формы записи комплексного числа:
алгебраическую и геометрическую. Есть еще показательная форма записи:

Если x<0,y<0 то

Есть замечательная формула Муавра, которая позволяет возвести комплексное число в
целую степень. Она была открыта французким математиком Абрахом де Муавром в 1707 году.
Выглядит она вот так:

В результате можем возвести число z в степень a:

Если Ваше комплексное число записано в показательном виде, то
можно использовать формулу:

Теперь, зная как находится модуль комплексного числа и формулу Муавра, можем найти
n корень из комплексного числа:

Здесь k это числа от 0 до n-1
Из этого можно сделать вывод, что существует ровно n различных корней n-ой
степени из комплексного числа.
Перейдем к синусу и косинусу.
Расчитать их нам поможет знаменитая формула Эйлера:

Кстати, еще существует тождество Эйлера, которое является частным
случаем формулы Эйлера при x=π:

Получаем формулы для вычисления синуса и косинуса:

Под конец статьи нельзя не упомянуть практическое применение комплексных
чисел, чтобы не возникало вопроса

сдались эти комплексные числа?
Ответ: в некоторых областях науки без них никак.
В физике в квантовой механике есть такое понятие как волновая функция, которая сама по себе комплекснозначна.
В электротехнике комплексные числа нашли себя в качестве удобной замены дифурам, которые неизбежно возникают при решении задач с линейными цепями переменного тока.
В теореме Жуковского (подъемная сила крыла) тоже используются комплексные числа.
А еще в биологии, медицине, экономике и еще много где.
Надеюсь, теперь вы умеете оперировать комплексными числами и сможете
применять их на практике.
Если что-то в статье непонятно — пишите в комментариях, отвечу.

Действия над комплексными числами, заданными в алгебраической форме

Алгебраическая форма комплексного числа

Как отмечалось ранее, комплексное число можно задавать в виде или . Последующее изучение комплексных чисел показывает, что комплексные числа можно задавать и другими способами.

Комплексное число, заданное в виде , называется комплексным числом в алгебраической форме.

Рассмотрим действия над комплексными числами, заданными в алгебраической форме.

Сложение комплексных чисел

Определение. Суммой двух комплексных чисел называется такое комплексное число, действительная часть которого равняется сумме действительных частей слагаемых, а мнимая часть – сумме мнимых частей слагаемых, то есть

Следовательно, чтобы сложить два комплексных числа, нужно сложить их действительные части, что дает действительную часть суммы, и сложить мнимые части, что дает мнимую часть суммы.

Сумма комплексно-сопряжённых чисел всегда является действительным числом.

Свойства суммы комплексных чисел

1. Сложение комплексных чисел является коммутативным, то есть для любых комплексных чисел справедливо равенство

2. Сложение комплексных чисел является ассоциативным, то есть для любых комплексных чисел справедливо равенство

Возможно вам будут полезны данные страницы:

Вычитание комплексных чисел

Определение. Разностью двух комплексных чисел называется такое число, которое в сумме с вычитаемым дает уменьшаемое.

Вычитание комплексных чисел является всегда возможным.

Теорема Для любых комплексных чисел всегда существует разность , определяемая однозначно.

Докажем, что существует такое число , которое удовлетворяет условию , то есть что или . На основании равенства комплексных чисел приходим к системе уравнений

Эта система уравнений имеет решение, и к тому же лишь одно, а именно:

что и нужно было доказать.

Следовательно, разность двух комплексных чисел – это такое комплексное число, действительная и мнимая части которого равняются соответственно разности действительных и мнимых частей уменьшаемого и вычитаемого, то есть

Разность комплексно-сопряжённых чисел всегда является мнимым числом.

Умножение комплексных чисел

Определение. Произведением двух комплексных чисел и называется комплексное число, определяемое формулой

Практически, чтобы умножить комплексные числа, следует умножить их по правилу умножения многочленов, заменив при этом на -1, и привести подобные члены.

Произведение комплексно-сопряжённых чисел всегда является действительным числом.

Свойства произведения комплексных чисел

1. Умножение комплексных чисел является коммутативным, то есть для любых комплексных чисел справедливо равенство

2. Умножение комплексных чисел является ассоциативным, то есть для любых комплексных чисел справедливо равенство

3. Умножение комплексных чисел является дистрибутивным относительно сложения, то есть для любых комплексных чисел справедливо равенство

Деление комплексных чисел

Определение. Частным от деления комплексных чисел называется такое комплексное число, которое в произведении с делителем дает делимое, если делитель отличается от нуля.

Докажем, что всегда существует частное от деления двух комплексных чисел, если знаменатель отличается от нуля.

Теорема Частное определяется однозначно для любых комплексных чисел если

Пусть . Докажем, что существуют такие числа х и у, которые удовлетворяют уравнению Выполнив умножение, получим:

Исходя из равенства комплексных чисел, имеем систему уравнений

Решив эту систему уравнений, находим

Следовательно, система уравнений имеет решение, и к тому же единственное. Тогда

ЗАМЕЧАНИЕ. Деление комплексных чисел в алгебраической форме удобно выполнять следующим образом. Числитель и знаменатель следует умножить на число, комплексно-сопряженное знаменателю, после чего в числителе и знаменателе выполнить умножение комплексных чисел по правилу умножения многочленов. Полученный результат записать в алгебраической форме.

Примеры с решением

Использовав формулы (2.1), (2.2), (2.5), (2.6), получим:

Пример задачи с решением 2

Найти значение выражения

Воспользовавшись правилом умножения многочленов, имеем

Воспользуемся правилом умножения многочленов:

4) По формуле (2.8) имеем:

Деление комплексных чисел можно выполнять по формуле (2.13), но проще это сделать, умножив числитель и знаменатель на число, комплексносопряжённое знаменателю.

Что такое комплексное число

Комплексные числа — это числа вида

— мнимая единица, то есть число, для которого выполняется равенство:

Понятие о комплексном числе

Процесс расширения понятия числа от натуральных к действительным был связан как с потребностями практики, так и с нуждами самой математики. Сначала для счета предметов использовались натуральные числа. Необходимость выполнения деления привела к понятию обыкновенной (и десятичной) дроби, необходимость выполнения вычитания — к понятиям нуля и отрицательного числа, необходимость извлечения корней из положительных чисел — к понятию иррационального числа.

Все перечисленные операции выполнимы на множестве действительных чисел. Однако остались и невыполнимые на этом множестве операции, например извлечение квадратного корня из отрицательного числа. Значит, имеется потребность в дальнейшем расширении понятия числа, в появлении новых чисел, отличных от действительных.

Геометрически действительные числа изображаются точками на координатной прямой: каждому действительному числу соответствует одна точка прямой («образ» действительного числа) и, обратно, каждая точка координатной прямой соответствует одному действительному числу. Координатная прямая сплошь заполнена образами действительных чисел, т. е., выражаясь фигурально, «на ней нет места для новых чисел». Возникает предположение о том, что геометрические образы новых чисел надо искать уже не на прямой, а на плоскости. Однако каждую точку М координатной плоскости ху можно отождествить с координатами этой точки. Поэтому естественно в качестве новых чисел ввести упорядоченные пары действительных чисел (упорядоченные в том смысле, что

Комплексным числом называют всякую упорядоченную пару

называют равными тогда и только тогда, когда

Арифметические операции над комплексными числами

Суммой комплексных чисел

называют комплексное число

Комплексным нулем считают пару (0; 0). Числом, противоположным числу

Разностью комплексных чисел

называют, как обычно, такое число

Разность всегда существует и единственна. В самом деле, пусть

Это значит, что

Таким образом, получаем следующее правило вычитания комплексных чисел:

Например, (9; 10) – (8; 12) = (9 – 8; 10 – 12) = (1;-2).

Произведением комплексных чисел

Арифметические операции над комплексными числами обладают теми же свойствами, что арифметические операции над действительными числами (см. п. 29).

Существует, и только одно, комплексное число

Из этой системы двух уравнений с двумя переменными находим (см. п. 164)

Получили следующее правило деления комплексных чисел: если

Алгебраическая форма комплексного числа

Используя введенные в п. 45 определения сложения и умножения комплексных чисел, легко получить следующие равенства:

, а комплексное число (0; 1) обозначать буквой

и называть мнимой единицей. Тогда равенство (1) принимает вид

а равенство (2) — вид

называют алгебраической формой комплексного числа

при этом число

Если мнимая часть комплексного числа

отлична от нуля, то число называют мнимым, если при этом

= 0, т. е. число имеет вид bi, то его называют чисто мнимым, наконец, если у комплексного числа

мнимая часть равна нулю, то получается действительное число

Алгебраическая форма существенно облегчает выполнение арифметических операций над комплексными числами.

Сложение. Известно (см. п. 45), что

Выполнив сложение тех же чисел в алгебраической форме, считая

Сравнивая равенства (7) и (8), замечаем, что получился верный результат.

Вычитание. Известно (см. п. 45), что

Выполнив вычитание тех же чисел в алгебраической форме, считая

Сравнивая равенства (9) и (10), замечаем, что получился верный результат.

Умножение. Известно (см. п. 45), что

Выполнив умножение тех же чисел в алгебраической форме, считая

Воспользуемся тем, что

(см. равенство (5)); тогда

Сравнивая равенства (11) и (12), замечаем, что получился верный результат.

Деление. Известно (см. п. 45), что если

Выполним деление тех же чисел в алгебраической форме, считая

и с + di обычными двучленами, a

Сравнивая равенства (13) и (14), замечаем, что получился верный результат.

Подводя итоги, приходим к следующему важному практическому выводу: над комплексными числами, записанными в алгебраической форме, можно осуществлять все арифметические операции как над обычными двучленами, учитывая лишь, что

Чтобы преобразовать в комплексное число дробь вида

нужно числитель и знаменатель дроби умножить на число с — di; числа с + di и с – di называют комплексно-сопряженными.

Пример 1.

Пример 2.

Пример 3.

Найти действительные числа х и у такие, что выполняется равенство

равны тогда и только тогда, когда равны их действительные части (

из которой находим (см. п. 164)

Пример 4.

Найти комплексные числа z, удовлетворяющие равенству

Будем искать комплексное число z в виде х + yi. Имеем

Из последнего равенства следует, что

Эта система имеет два решения (см. п. 164): (2; 3) и (-2; -3). Значит,

Пример 5.

Имеем (см. п. 58)

Отыскание комплексных корней уравнений

Тем самым мы получаем возможность извлекать квадратные корни из отрицательных действительных чисел. Это позволяет находить не только действительные, но и мнимые корни уравнений.

Имеем (см. п. 137)

Значит, либо х – 2 = 0, откуда находим

Эта лекция взята со страницы полного курса лекций по изучению предмета “Математика”:

Наталья Игоревна Восковская

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Выделяют три формы представления (записи) комплексных чисел:

• алгебраическая;
• тригонометрическая;
• показательная.

Запись некоторого комплексного числа $z$ в виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:

• $a$ – вещественная (действительная) часть, обозначение $Rez=a$;
• $b$ – мнимая часть, обозначение $Imz=b$.

Сделаем домашку
с вашим ребенком за 380 ₽

Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online

Представление комплексно-сопряженного числа $z=a-bi$ в алгебраической форме записи имеет вид $z=a+(-b)i$.

Действительное число в алгебраической форме записывается как $z=a+0cdot i$, чисто мнимое – $z=0+bcdot i$.

Представить заданные комплексные числа в алгебраической форме:

Алгебраическая форма представления некоторого комплексного числа имеет вид $z=a+bi$.

Следовательно, в алгебраической форме число $z$ записывается следующим образом

2) Преобразуем исходное число, раскрыв скобки и выполнив необходимые вычисления:

«Формы записи комплексных чисел» 👇

2) В исходном комплексном числе $z$ имеем $a=0,b=3$.

Представить в тригонометрической форме заданные комплексные числа, для которых:

Тригонометрическая форма представления некоторого комплексного числа имеет вид $z=r(cos arphi +icdot sin arphi )$.

Для $r=2,arphi =pi $ получаем комплексное число $z=2cdot (cos pi +icdot sin pi )$.

Вычислим модуль исходного комплексного числа:

Вычислим аргумент исходного комплексного числа:

Подставим полученные значения и получим:

Представить в показательной форме заданные комплексные числа, для которых:

Представить заданные комплексные числа в показательной форме:

1) По условию $a=4,b=0$.

Чтобы комплексное число $z$, записанное в тригонометрической форме, привести к алгебраической форме записи, необходимо выполнить следующее:

• подставить в запись числа соответствующие значения для $cos arphi $ и $sin arphi $ (использовать таблицы Брадиса);
• преобразовать полученное выражение к алгебраической форме записи, выполнив при необходимости соответствующие вычисления.

Алгебраическая форма записи некоторого комплексного числа имеет вид $z=a+bi$.

1) По таблице косинусов и синусов $cos 2pi =1;sin 2pi =0$.

Подставим значения и выполним преобразования и вычисления:

Следовательно, $z=3+0cdot i$ – искомая запись комплексного числа.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Найдём
модуль этого числа: 
 Аргумент
данного числа находится из системы Значит,
один из аргументов числа 
 равен  
Получаем: Ответ.

Модуль
комплексного числа

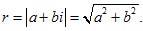
Модуль
действительного числа совпадает с его
абсолютным значением. Сопряженные
комплексные числа а + bi и a – bi имеют один
и тот же модуль.

Угол
φ между осью а

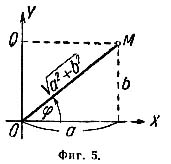
бсцисс
и вектором ОМ, изображающим комплексное
число а + bi, называется аргументом
комплексного числа а + bi. На фиг. 6 вектор
OM изображает комплексное число -3 -3i.
Угол

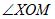
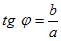
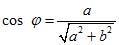
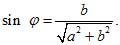
Однако
ни одна из них в отдельности не позволяет
найти аргумент по абсциссе и ординате
(см. примеры).

Пример
1.Найти аргумент комплексного числа –
3 – 3i.

По
формуле (

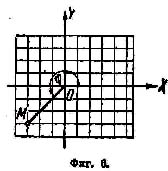
2)tgφ
= -3/-3 = 1. Этому условию удовлетворяют
как угол 45˚, так и угол 225˚. Но угол 45˚
не является аргументом числа – 3 – 3i.
(фиг. 6). Правильный ответ будет φ = 225˚
(или —135˚, или 585˚ т. д.). Этот результат
получится если учесть, что абсцисса и
ордината данного комплексного числа
отрицательны. Значит, точка M лежит в
третьей четверти.

Другой
способ. По формуле (3) находим

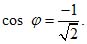
Формула
(4) показывает, что sin φ тоже отрицателен.
Значит, угол φ принадлежит третьей
четверти, так что φ = 225˚ ±
360˚k.

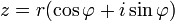
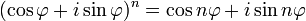
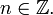
13)Показательная форма комплексного числа

Рассмотрим
тригонометрическую форму комплексного
числа

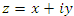
Используя
формулу Эйлера, преобразуем правую
часть равенства (1):

Запись
вида (2) называется показательной
формой комплексного
числа.

Существует
также показательная форма комплексного
числа связанная с тригонометрической
по формуле Эйлера:

Данное
соотношение легко доказать, если
произвести разложение экспоненты в
ряд Тейлора:

Представим
ряд в виде суммы четных и нечетных
членов последовательности:

Рассмотрим
более подробно мнимую единицу в четной
и нечетной степенях. Выражение (1)
задало

,
в свою очередь

Построим
аналогичным облразом рекурентное
соотношение для нечетных степеней:

Таким
образом выражение (11) с учетом (12) и (13)
принимает вид:

В
выражении (14) первая сумма по четным
степеням дает разложение в ряд Тейлора
функции косинуса, а вторая сумма по
нечетным степеням дает разложение в
ряд Тейлора функции синуса. Таким
образом, получено доказательство
справедливости формулы Эйлера (9).
Используя формулу Эйлера можно сделать
ряд важных замечаний: Замечание 1:

Тригонометрическая форма комплексного числа

Любое комплексное число (за искл. нуля) вида z = a + bi можно записать в тригонометрической форме следующим образом:

Чтобы было понятнее, покажем комплексное число на координатной плоскости. При этом, в качестве примера будем исходить из того, что и больше нуля.

Исходя из теоремы Пифагора модуль вычисляется так:

Аргумент комплексного числа () – угол между положительной полуосью действительной оси (RE) и вектором, который проведен из начала координат. Аргумент не существует для = 0, может обозначаться как arg .

Формула для расчета аргумента зависит от того, какие значения принимают и .

Пример: представим в тригонометрической форме комплексное число z = 3i.

Решение: = 0, = 3, следовательно:

Т.к. = 0, значит вектор совпадает с осью ординат (направлен вверх), следовательно = 90°.

Таким образом, тригонометрическая форма числа z = 3i выглядит так:z = 3 ⋅ (cos 90° + i ⋅ sin 90°)

Любое комплексное число (за искл. нуля) вида z = a + bi можно записать в показательной форме:

• – модуль комплексного числа;
• – его аргумент.

Примечание: показательная форма используется намного реже, чем тригонометрическая, поэтому базовой информации выше в большинстве случаев должно быть достаточно.

Над комплексными числами можно проводить различные операции, а именно:

• Складывать и вычитать
• Умножать и делить
• Извлекать корни и возводить в степень
• Переводить из одной формы в другую

Для нахождения суммы и разности складывается и вычитаются только соответствующие друг другу члены. Мнимая часть только с мнимой, а действительная только с действительной:

$$ z_1 + z_2 = (a_1+ib_1) + (a_2+ib_2) = (a_1 + a_2)+i(b_1 + b_2) $$

$$ z_1 – z_2 = (a_1+ib_1) – (a_2+ib_2) = (a_1 – a_2)+i(b_1 – b_2) $$

Умножение в алгебраической форме:

$$ z_1 cdot z_2 = (a_1+ib_1) cdot (a_2+ib_2) = (a_1 a_2 – b_1 b_2)+i(a_1 b_2 + a_2 b_1) $$

Умножение в показательной форме:

Деление в алгебраической форме:

Деление в показательной форме:

Для возведения в степень необходимо умножить комплексное число само на себя необходимое количество раз, либо воспользоваться формулой Муавра:

Для извлечения корней необходимо также воспользоваться формулой Муавра:

Так же теория комплексных чисел помогает находить корни многочленов. Например, в квадратном уравнении, если $ D<0 $, то вещественных корней нет, но есть комплексные. В последнем примере рассмотрен данный случай.

Рассмотрим на практике комплексные числа: примеры с решением.

Изображение

Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:

Аргумент обозначается $ arphi $.

Аргумент комплексного числа $ arphi $ нужно находить по различным формулам в зависимости от полуплоскости, в которой лежит само число.

Формы

Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:

Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.

Комплексные числа

Принято записывать мнимую часть комплексного числа как $ Im(z) = b $, а действительную $ Re(z) = a $.

Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.

На множестве действительных чисел ряд алгебраических задач, в частности нахождение корней квадратных уравнений с отрицательным дискриминантом, не имеет решения. Введём некоторое навое число, которое будем считать решением уравнения х2 + 1 = 0. Корень уравнения  х2 + 1 = 0 или  х2 = -1 называется мнимой единицей и обозначается буквой i. Таким образом i2 = -1.

В некоторых технических дисциплинах мнимую единицу обозначают буквой j. В дальнейшем будем использовать оба обозначения.

Мнимая единица позволяет ввести числа нового вида, которые называют комплексными.

Комплексным числом называют выражение вида

называют действительной, а число

— мнимой частями комплексного числа. Комплексное число, как правило, обозначают буквой

. Два комплексных числа

называют равными тогда и только тогда, когда

Понятия “больше” и “меньше” для комплексных чисел не определено. Комплексное число

называется нулём и обозначается 0; комплексное число

отождествляется с действительным числом

называют чисто мнимым и обозначают

называются сопряжёнными и обозначаются

. Например, в числе

, сопряжённым к нему будет число

, а для числа

сопряжённым будет число

Множество комплексных чисел принято обозначать буквой С. Запись комплексного числа в виде

называется алгебраической формой комплексного числа.

Действия над комплексными числами в алгебраической форме

Сложение, вычитание, умножение комплексных чисел в алгебраической форме по правилам соответствующих действий над многочленами.

Пример 1. Найти сумму и произведение комплексных чисел

Решение: Сумму находим формальным сложением двучленов

произведение находим перемножив двучлены

с последующей заменой

Легко увидеть, что слагаемое двух сопряжённых чисел является действительным числом:

Воспользуемся этим свойством для введения действия деления двух комплексных чисел.

При делении комплексных чисел

достаточно умножить числитель и знаменатель дроби

на число сопряжённое к знаменателю, то есть на

Пример 2. Даны комплексные числа

Находим разность вычитанием двучленов

Чтобы найти частное

Действия над комплексными числами имеют следующие интересные свойства:

Доказательство выходит из определения сопряжённых чисел. Действительно,

Аналогично доказываются и другие приведённые свойства.

Возведение комплексного числа в степень выполняется по формулам возведения двучлена в степень. При этом следует учитывать, что

Пример 3. Найти комплексное число

Выполнив в знаменателе возведение в степень, получим:

Умножив числитель и знаменатель на число, сопряжённое к знаменателю, то есть на -5-12i, получим:

Ответ: z = i.

Геометрическая интерпретация комплексного числа

Каждому комплексному числу

можно поставить в соответствие упорядоченную пару действительных чисел

Следовательно, комплексное число вида

изображается на координатной плоскости точкой

или вектором, начало которого совпадает с началом координат, а конец с т. М.

Сама координата плоскости называется при этом комплексной плоскости, ось абсцисс — действительной осью, ось ординат — мнимой осью.

Например, изобразим числа

Представление комплексного числа как вектора на плоскости позволяет ввести понятие модуля и аргумента комплексного числа.

Модулем комплексного числа называют длину вектора, которая соответствует данному числу (обозначают r либо p).

называют величину угла

между положительным направлением действительной оси и вектора, который соответствует данному комплексному числу.

На основе теоремы Пифагора получаем

Например, комплексное число

, в отличии от модуля, вычисляется неоднозначно. Так аргументом числа 5 являются следующие углы

Среди бесконечного множества значений аргумента только одно принадлежит промежутку

. Эти значения аргумента мы и будем вычислять.

Аргумент легко вычислить, если комплексное число расположено в I четверти. Действительно, согласно тригонометрическим соотношениям в прямоугольном треугольнике (рис. 2) имеем:

Если комплексные числа размещены в других четвертях, то необходимо провести дополнительные рассуждения. Рассмотрим рис. 3. Видим, что для

Таким образом, алгоритм нахождения аргумента комплексного числа следующий:

3. Установить, в какой четверти расположено комплексное число.

4. Вычислить аргумент

согласно приведённым формулам.

Возможны и другие способы нахождения аргумента комплексного числа, например:

Пример 4. Найти аргумент комплексного числа

Рассмотрим рис. 2. Согласно тригонометрическим соотношениям в прямоугольном треугольнике числа

можно выразить через r и

Тогда комплексное число запишется в виде:

Запись комплексного числа в таком виде называется тригонометрической формой комплексного числа.

Следовательно, для того, чтобы перейти от алгебраической формы записи комплексного  числа

Пример 5. Записать число

Найдём острый угол

Вектор, который соответствует данному комплексному числу принадлежит третьей четверти, поэтому аргумент равен

Для того, чтобы перейти от тригонометрической формы записи комплексного числа

к алгебраической, достаточно найти действительные числа

Пример 6. Записать число

Действия над комплексными числами в тригонометрической форме

В тригонометрической форме записи комплексного числа выполняют действия умножения, деления, возведения в степень, извлечения корня n-й степени. Выведение формул, по которым выполняются действия, относительно просты и основываются на основных формулах тригонометрии.

Следовательно, при умножении комплексных чисел, заданных в тригонометрической форме, их модули перемножают, а аргументы складывают; при делении — модули делят, а аргументы вычитают.

Правило умножения комплексных чисел автоматически распространяется на произвольное число множителей. Если взять равные множители

Полученную формулу называют формулой Муавра.

Для извлечении корня n-й степени из комплексного числа

Ответ записать в алгебраической форме.

. Ответ запишите в алгебраической и тригонометрической формах.

Решение: Запишем число -81 в тригонометрической форме:

для комплексной переменной, известный математик Л. Эйлер установил соотношение

Из заданной формулы следует, что каждое комплексное число

можно записать в виде

которое называется показательной формой записи.

Над комплексными числами в показательной форме выполняют те же действия что и в тригонометрической форме. Выведение формул, по которым выполняют действия основывается на основных свойствах степени.

Пример 11. Представить число

Решение: Согласно условию задачи

Пример 12. Выполнить действия, результат записать в тригонометрической и показательной формах:

Решение: Сначала выполним действия:

Теперь полученное число запишем в тригонометрической и показательной формах. Для этого найдём модуль и аргумент:

Перевести из алгебраической в тригонометрическую и показательную форму:$$ z = 4-4i $$

Вычислить сумму и разность заданных комплексных чисел:$$ z_1 = 3+i, z_2 = 5-2i $$

Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел:$$ z_1 + z_2 = (3+i) + (5-2i) = (3+5)+(i-2i) = 8 – i $$Аналогично выполним вычитание чисел:$$ z_1 – z_2 = (3+i) – (5-2i) = (3-5)+(i+2i) = -2 + 3i $$

$$ z_1 + z_2 = 8 – i; z_1 – z_2 = -2 + 3i $$

Выполнить умножение и деление комплексных чисел:$$ z_1 = 3+i, z_2 = 5-2i $$

Возвести комплексное число $ z = 3+3i $ в степень: a) $ n=2 $ б) $ n=7 $

$$ z^2 = (3+i)^2 = 18i $$ $$ z^7 = 17496(1-i) $$

$$ x_1 = -1 – i; x_2 = -1 – i $$

В статье “Комплексные числа: примеры с решением” было дано определение, основные понятия, формы записи, алгебраические операции и решение практических примеров.