Какой коэффициент используется при любом значении прямой?. Почему прямые и параллельные плоскости не пересекаются в пространстве

параллельна
плоскости

лежит в плоскости

0(2; -4; -1) Рё
середину отрезка прямой

, заключенного между плоскостями

0(2; -3; -5) перпендикулярно
к плоскости

0(1; -1; -1) перпендикулярно
Рє РїСЂСЏРјРѕР№

0(1; -2; 1) перпендикулярно
Рє РїСЂСЏРјРѕР№

лежит
в плоскости

перпендикулярна к
РїСЂСЏРјРѕР№

перпендикулярна к
плоскости

0(28; -30; -27)
со скоростью v=12,5 по
перпендикуляру, опущенного из точки М0

1(1; 2; -3) параллельно
прямым

Доказать,
что если две прямые , пересекаются, то уравнение
плоскости, в которой они лежат, может быть
представлено в следующем виде:

перпендикулярно к плоскости

Рё
пересекает прямую

1 Прямая параллельна плоскости

Прямая
параллельна плоскости, если она не имеет
с плоскостью общих точек. На рис. 5 прямая
l параллельна плоскости π.

Рис.
5. Прямая параллельна плоскости

Давайте
посмотрим, как работает этот признак.
Пусть

– треугольная призма, в которой проведена
плоскость

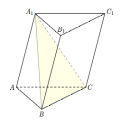
Рис. 6. Прямая

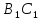
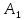
Поскольку
боковые грани призмы являются
параллелограммами, имеем

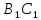
║BC.
Но прямая BC лежит в плоскости

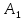
BC.
Поэтому в силу признака параллельности
прямой и плоскости мы заключаем, что
прямая

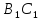
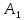
Другое
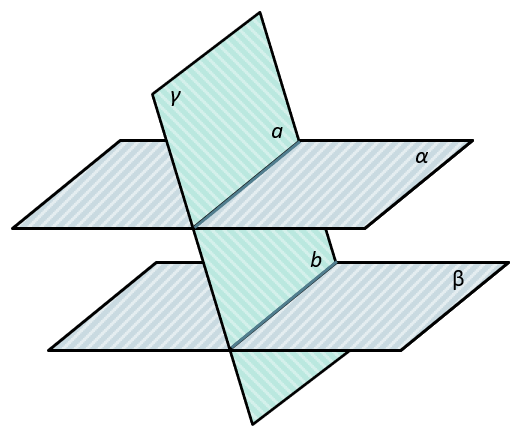
важное утверждение, которое нередко
используется в задачах, – это теорема о
пересечении двух плоскостей, одна из
которых проходит через прямую, параллельную
другой плоскости.

Теорема.
Пусть прямая l параллельна плоскости
π.
Если плоскость σ проходит через прямую
l и пересекает плоскость π по прямой m,
то m║l.

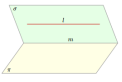
Рис. 7. К теореме

Если
прямая параллельна плоскости,
то точка

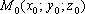
(а,
значит, и любая точка данной прямой) не
удовлетворяет уравнению
плоскости:

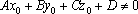
Таким
образом, условие параллельности прямой
и плоскости записывается следующей
системой:

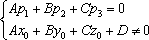
2 Прямая пересекает плоскость

Если
прямая не лежит в плоскости и не
параллельна ей, она пересекает плоскость.

Прямая
пересекает плоскость тогда
и только тогда, когда её направляющий
вектор

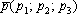
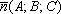
Из
утверждения следует, что скалярное
произведение вектора
нормали и направляющего вектора
будет отлично
от нуля:

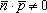
В
координатах условие запишется следующим
образом:

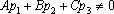
Если
же данные векторы ортогональны,
то есть
если их скалярное
произведение равно
нулю:

,
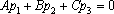
то прямая либо параллельна плоскости,
либо лежит в ней:

Важным
частным случаем пересечения прямой и
плоскости является их перпендикулярность.

Интуитивно
вам совершенно ясно, что значит «прямая
перпендикулярна плоскости», но определение
нужно знать обязательно.

Определение:
прямая называется перпендикулярной
плоскости, если она перпендикулярна
любой прямой, лежащей в этой плоскости.

Предположим,
в конкретной задаче нам хочется доказать,
что прямая l перпендикулярна плоскости
π. Как действовать? Не будем же мы
перебирать все прямые, лежащие в плоскости
π! К счастью, это и не нужно. Оказывается,
достаточно предъявить две пересекающиеся
прямые плоскости π, перпендикулярные
прямой l.

3 Прямая лежит в плоскости

Прямая
лежит в плоскости, если каждая точка
прямой принадлежит этой плоскости. На
рисунке 8 прямая l лежит в плоскости π.
В таком случае говорят ещё, что плоскость
π проходит через прямую l.

Если
прямая лежит в плоскости,
то
точка

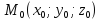
(а, значит, и любая точка данной
прямой) удовлетворяет уравнению
плоскости:

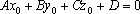
Аналитические
условия данного случая запишутся похожей
системой:

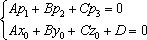
перпендикулярно
плоскости

пучку
плоскостей

принадлежит
пучку плоскостей

Написать уравнение
плоскости, которая принадлежит пучку плоскостей

РЅР°
плоскость

В данной статье будут изучены вопросы параллельности плоскостей. Дадим определение плоскостям, которые параллельны между собой; обозначим признаки и достаточные условия параллельности; рассмотрим теорию на иллюстрациях и практических примерах.

Параллельные плоскости

Параллельные плоскости – плоскости, не имеющие общих точек.

Чтобы обозначить параллельность применяют такой символ: ∥. Если заданы две плоскости: α и β, являющиеся параллельными, краткая запись об этом будет выглядеть так: α ‖ β.

На чертеже, как правило, плоскости, параллельные друг другу, отображаются как два равных параллелограмма, имеющих смещение относительно друг друга.

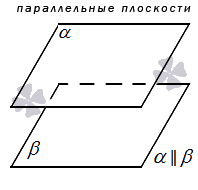
В речи параллельность можно обозначить так: плоскости α и β параллельны, а также – плоскость α параллельна плоскости β или плоскость β параллельна плоскости α.

Признак и условия параллельности

В процессе решения геометрических задач зачастую возникает вопрос: а параллельны ли заданные плоскости между собой? Для получения ответа на этот вопрос используют признак параллельности, который также является достаточным условием параллельности плоскостей. Запишем его как теорему.

Плоскости являются параллельными, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Доказательство этой теоремы приводится в программе геометрии за 10-11 класс.

В практике для доказательства параллельности, в том числе, применяют две следующие теоремы.

Если одна из параллельных плоскостей параллельна третьей плоскости, то другая плоскость или также параллельна этой плоскости, или совпадает с ней.

Если две несовпадающие плоскости перпендикулярны некоторой прямой, то они параллельны.

На основе этих теорем и самого признака параллельности доказывается факт параллельности любых двух плоскостей.

Рассмотрим подробнее необходимое и достаточное условие параллельности плоскостей α и β, заданных в прямоугольной системе координат трехмерного пространства.

Допустим, что в некоторой прямоугольной системе координат задана плоскость α, которой соответствует общее уравнение  A1x+B1y+C1z+D1=0, а также задана плоскость β, которую определяет общее уравнение вида A2x+B2y+C2z+D2=0  .

Для параллельности заданных плоскостей α и β необходимо и достаточно, чтобы система линейных уравнений A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 не имела решения (являлась несовместной).

Предположим, что заданные плоскости, определяемые уравнениями A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0 являются параллельными, а значит не имеют общих точек. Таким образом, не существует ни одной точки в прямоугольной системе координат трехмерного пространства, координаты которой отвечали бы условиям одновременно обоих уравнений плоскостей, т.е. система A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 не имеет решения. Если указанная система не имеет решений, тогда не существует ни одной точки в прямоугольной системе координат трехмерного пространства, чьи координаты одновременно отвечали бы условиям обоих уравнений системы. Следовательно, плоскости, заданные уравнениями A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0 не имеют ни одной общей точки, т.е. они параллельны.

Разберем использование необходимого и достаточного условия параллельности плоскостей.

Заданы две плоскости: 2x+3y+z-1=0 и 23x+y+13z+4=0. Необходимо определить, являются ли они параллельными.

Запишем систему уравнений из заданных условий:

Проверим, возможно ли решить полученную систему линейных уравнений.

Ранг матрицы 23123113 равен одному, поскольку миноры второго порядка равны нулю. Ранг матрицы 231123113-4 равен двум, поскольку минор 2123-4 отличен от нуля. Таким образом, ранг основной матрицы системы уравнений меньше, чем ранг расширенной матрицы системы.

Совместно с этим, из теоремы Кронекера-Капелли следует: система уравнений 2x+3y+z-1=023x+y+13z+4=0не имеет решений. Этим фактом доказывается, что плоскости 2x+3y+z-1=0 и 23x+y+13z+4=0 являются параллельными.

Отметим, что, если бы мы применили для решения системы линейных уравнений метод Гаусса, это дало бы тот же результат.

Ответ: заданные плоскости параллельны.

Необходимое и достаточное условие параллельности плоскостей возможно описать по-другому.

Чтобы две несовпадающие плоскости α и β были параллельны друг другу необходимо и достаточно, чтобы нормальные векторы плоскостей α и β являлись коллинеарными.

Доказательство сформулированного условия базируется на определении нормального вектора плоскости.

Таким образом, чтобы несовпадающие плоскости α и β с заданными выше нормальными векторами были параллельны, необходимо и достаточно, чтобы имело место действительное число t, для которого верно равенство:

В прямоугольной системе координат трехмерного пространства заданы плоскости α и β. Плоскость α проходит через точки: A(0, 1, 0), B(-3, 1, 1), C(-2, 2, -2). Плоскость β описывается уравнением x12+y32+z4=1Необходимо доказать параллельность заданных плоскостей.

Удостоверимся, что заданные плоскости не совпадают. Действительно, так и есть, поскольку координаты точки A не соответствуют уравнению плоскости β.

Для получения координат нормального вектора плоскости x12+y32+z4=1 приведем это уравнение к общему уравнению плоскости:

Ответ: плоскости α и β не совпадают; их нормальные векторы коллинеарные. Таким образом, плоскости α и β параллельны.

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Статья рассматривает понятия параллельность прямой  и плоскости. Будут рассмотрены основные определения и приведены примеры.  Рассмотрим признак параллельности прямой к плоскости с необходимыми и достаточными условиями параллельности, подробно решим примеры заданий.

Параллельные прямые и плоскость – основные сведения

Прямая и плоскость называются параллельными, если не имеют общих точек, то есть не пересекаются.

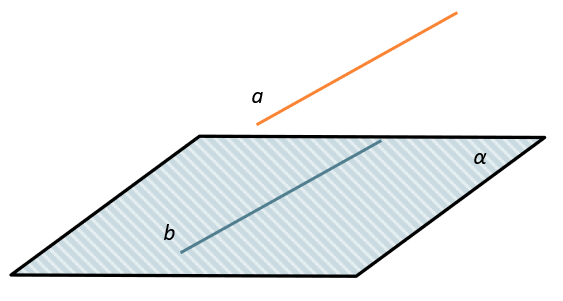
Параллельность обозначается «∥». Если в задании по условию прямая a и плоскость α параллельны, тогда обозначение имеет вид a∥α. Рассмотрим рисунок, приведенный ниже.

Считается, что прямая a, параллельная плоскости α и плоскость α, параллельная прямой a, равнозначные, то есть прямая и плоскость параллельны друг другу в любом случае.

Параллельность прямой и плоскости – признак и условия параллельности

Не всегда очевидно, что прямая и плоскость параллельны. Зачастую это нужно доказать. Необходимо использовать достаточное условие, которое даст гарантию на параллельность. Такой признак имеет название признака параллельности прямой и плоскости. Предварительно рекомендуется изучить определение параллельных прямых.

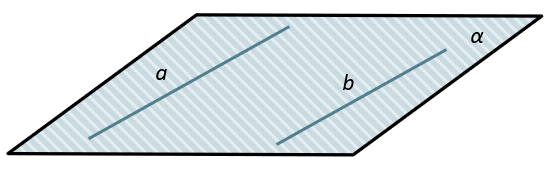
Если заданная прямая a, не лежащая в плоскости α, параллельна прямой b, которая принадлежит плоскости α, тогда прямая a параллельна плоскости α.

Рассмотрим теорему, используемую для установки параллельности прямой с плоскостью.

Если одна из двух параллельных прямых параллельна плоскости, то другая прямая лежит в этой плоскости либо параллельна ей.

Подробное доказательство рассмотрено в учебнике 10-11 класса по геометрии. Необходимым и достаточным условием параллельности прямой с плоскостью возможно при наличии определения направляющего вектора прямой и нормального вектора плоскости.

Для параллельности прямой a, не принадлежащей плоскости α, и данной плоскости необходимым и достаточным условием является перпендикулярность направляющего вектора прямой с нормальным вектором заданной плоскости.

Условие применимо, когда необходимо доказать параллельность в прямоугольной системе координат трехмерного пространства. Рассмотрим подробное доказательство.

Допустим, прямая а в систему координат Оху задается каноническими уравнениями прямой в пространстве , которые имеют вид x-x1ax=y-y1ay=z-z1az или параметрическими уравнениями прямой в пространстве x=x1+ax·λy=y1+ay·λz=z1+az·λ, плоскостью α с общими уравнениями плоскости Ax+By+Cz+D=0.

Определить, параллельны ли прямая x=1+2·λy=-2+3·λz=2-4·λ с плоскостью x+6y+5z+4=0.

Получаем, что предоставленная прямая не принадлежит плоскости, так как координаты прямой M(1, -2, 2) не подходят. При подстановке получаем, что 1+6·(-2)+5·2+4=0⇔3=0.

Ответ: прямая с плоскостью параллельны.

Определить параллельность прямой АВ в координатной плоскости Оуz, когда даны координаты A(2, 3, 0), B(4, -1, -7).

Отсюда следует, что прямая АВ с координатной плоскостью Оyz не являются параллельными.

Ответ: не параллельны.

Не всегда заданное условие способствует легкому определению доказательства параллельности прямой  и плоскости. Появляется необходимость в проверке принадлежности прямой a плоскости α. Существует еще одно достаточное условие, при помощи которого доказывается параллельность.

При заданной прямой a  с помощью уравнения  двух пересекающихся плоскостей A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0, плоскостью α – общим уравнением плоскости  Ax+By+Cz+D=0.

Необходимым и достаточным условием для параллельности прямой a и плоскости α яляется отсутствие решений системы линейных уравнений, имеющей вид A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0Ax+By+Cz+D=0.

Из определения следует, что прямая a с плоскостью α не должна иметь общих точек, то есть не пересекаться, только в этом случае они будут считаться параллельными. Значит, система координат Охуz не должна иметь точек, принадлежащих ей и удовлетворяющих всем уравнениям:

A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0, а также уравнению плоскости Ax+By+Cz+D=0.

Следовательно, система уравнений, имеющая вид A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0Ax+By+Cz+D=0, называется несовместной.

Верно обратное: при отсутствии решений системы A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0Ax+By+Cz+D=0 не существует точек в Охуz, удовлетворяющих всем заданным уравнениям одновременно. Получаем, что нет такой точки с координатами, которая могла бы сразу быть решениями всех уравнений A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 и уравнения Ax+By+Cz+D=0. Значит, имеем параллельность прямой и плоскости, так как отсутствуют их точки пересечения.

Система уравнений A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0Ax+By+Cz+D=0 не имеет решения, когда ранг основной матрицы меньше ранга расширенной. Это проверяется теоремой Кронекера-Капелли для решения линейных уравнений. Можно применять метод Гаусса для определения ее несовместимости.

Доказать , что прямая x-1=y+2-1=z3 параллельна плоскости 6x-5y+13z-23=0.

Для решения данного примера следует переходить от канонического уравнения прямой к виду уравнения двух пересекающихся плоскостей. Запишем это так:

Чтобы доказать параллельность заданной прямой x-y-2=03x+z=0 с плоскостью 6x-5y+13z-23=0 , необходимо уравнения преобразовать в систему уравнений x-y-2=03x+z=06x-5y+13z-23=0.

Видим, что она не решаема, значит прибегнем к методу Гаусса.

Расписав уравнения, получаем, что 1-10230106-51323~1-102031-60113-1113~1-102031-6000-913.

Отсюда делаем вывод, что система уравнений является несовместной, так как прямая и плоскость не пересекаются, то есть не имеют общих точек.

Делаем вывод, что прямая x-1=y+2-1=z3 и плоскость 6x-5y+13z-23=0 параллельны, так как было выполнено необходимое и достаточное условие для параллельности плоскости с заданной прямой.

Ответ: прямая и плоскость параллельны.

. Параллельность прямых и плоскостей в пространстве

С понятием «параллельность» вы познакомились при изучении планиметрии. Там оно относилось лишь к прямым. Выход в пространство, изменение «статуса» плоскости вынуждает нас не только уточнить определения некоторых понятий, но и расширить область их применения.

Две плоскости в пространстве называются параллельными, если они не имеют общих точек.

Прямая и плоскость в пространстве называются параллельными, если они не имеют общих точек.

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.

Как видим, первые два определения расширяют «зону действия» понятия «параллельность», а третье — уточняет старое определение. Ведь в пространстве две прямые могут и не принадлежать одной плоскости.

Две прямые, не принадлежащие одной плоскости, называются

На рисунке 17 изображена треугольная пирамида . Прямые и , и , и являются скрещивающимися, поскольку точки , , и не лежат в одной плоскости. Таким образом, противоположные рёбра треугольной пирамиды попарно скрещиваются (т. е. они лежат на скрещивающихся прямых).

Сформулируем и докажем несколько теорем о свойствах и признаках параллельности в пространстве.

о прямой, параллельной плоскости

, то любая плоскость, и пересекающая плоскость , пересекает её по прямой, параллельной

Пусть плоскость проходит через прямую и пересекается с плоскостью по прямой (рис. 18). Поскольку прямая параллельна плоскости , она не может пересекаться с прямой . Значит, эти прямые, согласно определению 3, параллельны.

(о двух параллельных плоскостях)

Если две плоскости параллельны, то любая плоскость, пересекающая одну из них, пересекает также и вторую, причём получившиеся при пересечении прямые параллельны.

Рассмотрим две параллельные плоскости и . Пусть  — некоторая точка плоскости (рис. 19, ). Рассмотрим плоскость , проходящую через точку . Пусть эта плоскость пересекает обе данные плоскости. Прямые, по которым плоскость пересекает и , не могут пересечься, следовательно, являются параллельными.

Осталось доказать, что плоскость , если она не совпадает с плоскостью , непременно пересекается с плоскостью . Предположим, что это не так (рис. 19, ). Возьмём любую точку в плоскости и проведём через точки и некоторую плоскость  так, чтобы она не содержала прямой, по которой пересекаются плоскости и . Это всегда можно сделать. Плоскость пересекает все три плоскости , и . В соответствии с только что доказанным получим, что в плоскости через точку проходят две прямые, параллельные одной и той же прямой (прямые, по которым плоскость пересекает плоскости и , параллельны прямой, по которой пересекаются плоскости и ), что противоречит известному нам свойству плоскости (свойство 4, § 5.1 из учебника 8 класса). Значит, плоскость пересекается с плоскостью .

В теореме 1.3 содержится утверждение, которое выделим отдельно.

Через любую точку пространства, не лежащую в данной плоскости, проходит не более одной плоскости, параллельной данной.

Это утверждение аналогично свойству параллельных прямых на плоскости.

признак параллельности прямой и плоскости

Если прямая, не лежащая в плоскости, параллельна какой-то прямой этой плоскости, то она параллельна и самой плоскости.

Пусть прямая , не лежащая в плоскости , параллельна прямой этой плоскости (рис. 20). Согласно определению две прямые и лежат в одной плоскости (обозначим эту плоскость через ) и не пересекаются. Это означает, что прямая не может пересечься с плоскостью , так как если они пересекаются, то точка их пересечения должна принадлежать плоскости . Отсюда следует, что прямые и пересекаются, что противоречит условию теоремы.

признак параллельности двух плоскостей

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то такие плоскости параллельны.

Пусть пересекающиеся прямые и плоскости соответственно параллельны прямым и плоскости  (рис. 21). Предположим, что эти плоскости пересекаются. Обозначим прямую, по которой они пересекаются, через . Эта прямая пересекается хотя бы с одной из заданных прямых плоскости . Пусть прямая пересекается с прямой . Но прямая параллельна плоскости (см. теорему 1.4) и не может пересекаться ни с какой прямой этой плоскости. Полученное противоречие доказывает теорему.

Через любую точку пространства, не принадлежащую данной плоскости, проходит единственная параллельная ей плоскость.

В самом деле, чтобы провести параллельную плоскость, нам достаточно построить две прямые, проходящие через точку и параллельные двум прямым в данной плоскости.

о двух плоскостях, проходящих через параллельные прямые

— две параллельные прямые. Рассмотрим две пересекающиеся плоскости , проходящие соответственно через прямые и не совпадающие с плоскостью, содержащей эти прямые. Тогда линия пересечения плоскостей

По признаку параллельности прямой и плоскости (теорема 1.4) прямая параллельна плоскости (  ), а прямая параллельна плоскости ( ). Теперь по теореме 1.2 линия пересечения плоскостей и параллельна как прямой , так и .

о транзитивности понятия параллельности для прямых

Если каждая из двух различных прямых параллельна третьей, то и сами эти прямые параллельны.

(Понятие «транзитивность» в математике означает перенос некоторого свойства: если рассматриваемое свойство выполняется для пары и и для пары и , то оно выполняется и для пары и . В данном случае , и  — это прямые, поэтому рассматриваемое свойство — параллельность прямых. При этом мы дополнительно требуем, чтобы и не совпадали.)

Пусть три прямые , и  таковы, что и   . Надо доказать, что .

Возьмём на прямой произвольную точку (рис. 22). Рассмотрим плоскости и : плоскость проходит через прямую и точку , плоскость  — через прямые и . Обозначим через линию пересечения  и . По теореме 1.6 имеем: и   . Но так как в плоскости через точку проходит единственная прямая, параллельная , то прямая совпадает с прямой . Теорема доказана.

Параллельность плоскостей

Две плоскости параллельны, если они не имеют общих точек.

Это определение. Однако в практических целях чаще используется признак параллельности плоскостей:

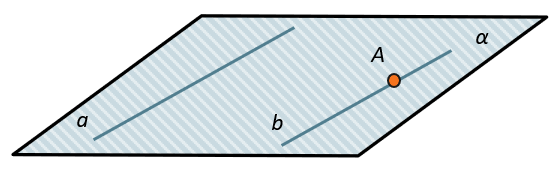
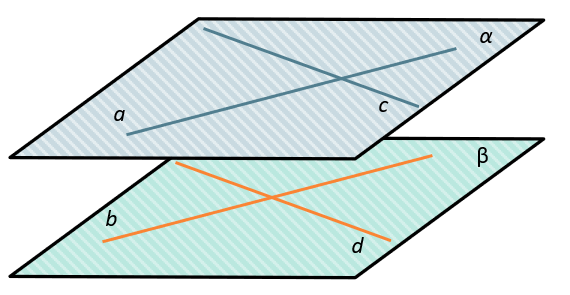
Плоскости параллельны друг другу, если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.

Свойства параллельных плоскостей:

• Если две плоскости параллельны третьей, то они параллельны друг другу.
• Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
• Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

Читаем дальше: Угол между плоскостями.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Параллельность плоскостей: признаки и свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Прямая и плоскость могут пересекаться или быть параллельными друг другу. Еще один случай — прямая лежит в плоскости.

Прямая параллельна плоскости, если она не имеет с плоскостью общих точек.

Это определение. Сложность только в одном — как на практике проверить, что бесконечная прямая нигде не пересечет бесконечную плоскость? Для практического применения используется признак параллельности прямой и плоскости:

Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости.

Этот признак часто используется в решении задач по стереометрии. Например, в правильной четырехугольной пирамиде SABCD прямая АВ параллельна прямой СD — значит, АВ параллельна всей плоскости SCD.

Читаем дальше: Угол между прямой и плоскостью.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Параллельность прямой иu0026nbsp;плоскости» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Параллельность прямых и плоскостей

Рассмотрим конфигурацию (расположение) прямых, прямой и плоскости, и плоскостей, при которых элементы параллельны друг другу.

Параллельные прямые – это прямые, лежащие в одной плоскости и не имеющие общих точек.

(a, b in alpha)

(a parallel b)

ТЕОРЕМЫ, СВЯЗАННЫЕ С ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ:

Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Если две прямые параллельны третьей прямой, то они параллельны между собой.

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Признак параллельности прямой и плоскости:

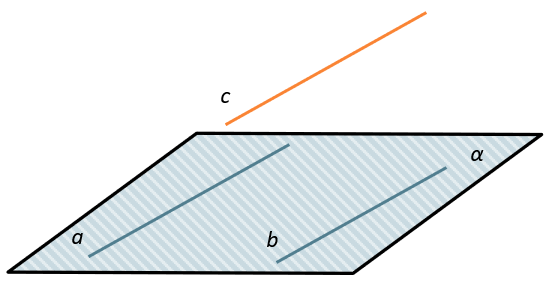
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

ТЕОРЕМЫ, СВЯЗАННЫЕ С ПРЯМОЙ, ПАРАЛЛЕЛЬНОЙ ПЛОСКОСТИ:

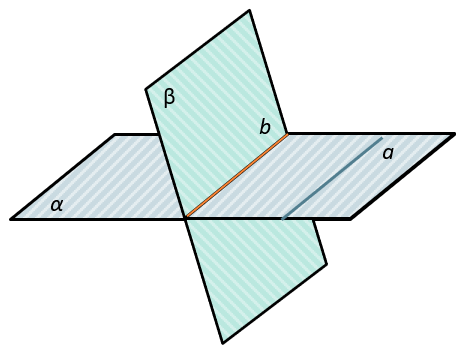
Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

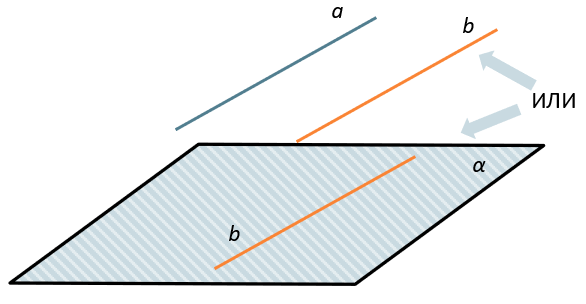
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, ЛИБО лежит в этой плоскости.

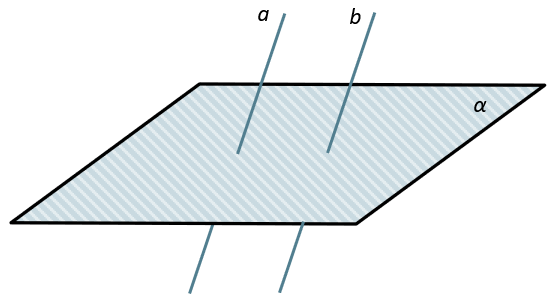
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.

Теорема о пересечении параллельных плоскостей третьей плоскостью:

Если две параллельные плоскости пересечены третьей, то линии пересечения плоскостей параллельны.

Прямая параллельна
плоскости, если она параллельна прямой,
принадлежащей этой плоскости (рис.37).

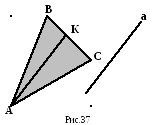
Для того чтобы
проверить, параллельна ли прямая заданной
плоскости, следует провести в этой
плоскости прямую, параллельную заданной.
Если такую прямую в плоскости построить
не удается, то заданные прямая и плоскость
не параллельны между собой.

4 Построение прямой линии, параллельной плоскости

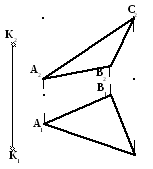
Дано: (АВС)
– о.п.

Построить прямую
а, проходящую через точку К, параллельно
плоскости треугольника (АВС)
и параллельно плоскости проекций П2.

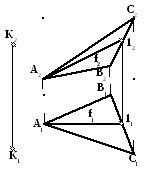
1. В плоскости 
проведите фронталь f
П2.
Построение начните с горизонтальной
проекции f1.

2. Найдите фронтальную
проекцию f2.

3. Через фронтальную
проекцию точки К2
проведите фронтальную проекцию прямой
а2,
параллельно f2

4. Через горизонтальную
проекцию точки К1
проведите а1,
параллельно f1

5 Перпендикулярность прямой и плоскости

При построении
перпендикуляра к плоскости необходимо
воспользоваться теоремой о проецировании
прямого угла и условием перпендикулярности
прямой к плоскости.