Понятие производного класса 11 и правила расчета. Производные основных элементарных функций. презентация к уроку математики (11 класс)

Производные некоторых элементарных функций

Основные правила дифференцирования

Производная сложной функции

Предел функции на бесконечности

Предел функции в точке

Приращение аргумента и функции

Средняя скорость изменения функции

Мгновенная скорость и понятие производной

Физический смысл производной

Геометрический смысл производной

Связь производной с возрастанием и убыванием функций

Производная как функция

Вторая производная функции и ее физический смысл

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Тема: Правила вычисления производной. Производные основных элементарных функций.

Цели и задачи: – закрепить понятия «производная функции»; – отработать применения правил нахождения производной функции при решении примеров; -развивать навыки логического мышления при выборе правил для вычисления производной.

эпиграф “При изучении наук примеры не менее поучительны, нежели правила” И. Ньютон “Примеры учат больше, чем теория”. М. Ломоносов

1.Проверка домашнего задания

Вспомнить математические термины, начинающиеся на эту букву

Правила вычисления производных Если функции U и V дифференцируемы в точке x 0 , то Если функция U дифференцируема в точке x 0 , а С-постоянная , то (С U)´=CU´ ( U + V ) ´ = U ´ + V ´ (U V) ´ = U ´ V + U V ´ U ´ U ´ V – U V ´ — = —————— V V 2

Функция Производная Устный счет

Таблица производных Элементарные функции Производные ( )’ ( ln х) ’ ( )’ * ln a (sin x)’ cos x (tg x)’ (cos x)’ -sin x (ctg x)’ –

Задание 1. Найдите производные функций: f(x)=3x+5 2. f(x)=4x 2 -5x 3 +9x 3 x 3. f(x)= — + — x 3 2 5 7 4 . f(x) = — + — – — x 2 x 3 x 5 . f(x) =

разминка «Кнопки мозга». Сложите ладони перед грудью пальцами вверх, не дышите, сдавите изо всех сил основания ладоней. Напряжены мускулы плеч и груди. Теперь втяните живот и потянитесь вверх. Как будто, опираясь на руки, выглядываете из окна. Всего 10-15 с и стало жарко. Повторите 3 раза.

Самостоятельная работа 1 вариант 2 вариант 1. f(x)=x 14 – x 12 + 3x 9 + x 3 – 9x 2 +5x 1. f(x)=x 13 – 2x 11 + 5x 8 + x 2 – x + 23 2. f(x)=2tg x + cos x– sin x 2. f(x)= ctg x + 2cos x + sin x 3. f(x)= 3. 4. f ( x )= x 10 · (7 x + 15) 4. f(x)=x 9 · (6x + 14); 5. f ( x )= 5. f(x)=

Понятие производной Алгебра и начала анализа 11 класс

Сегодня у нас праздник! Эпиграф: Был этот мир глубокой тьмой окутан. Был этот мир глубокой тьмой окутан. Да будет свет! И вот явился Ньютон. Да будет свет! И вот явился Ньютон. А.Поуп. Сегодня у нас праздник!

Что такое высшая математика? Что такое высшая математика? Когда она появилась? Когда она появилась? Что такое производная? Что такое производная?

Ответим на вопрос: Что такое скорость? Что такое скорость?

Очевидно, если t 0, то V ср. V мгн. Значит,

И еще: Одновременно, но независимо друг от друга они подошли к открытию анализа бесконечно малых. Одновременно, но независимо друг от друга они подошли к открытию анализа бесконечно малых.

А что такое касательная?

Задача о касательной к графику функции y = f(x) x y x0x0 М 0 (х 0,у 0 ) β А x М(х,у) С х=х-х 0 f(x) = f(x) – f(x 0 ) tgβ = При хх 0

y = f(x) y x0x0 М 0 (х 0,у 0 ) β А x М(х,у) С х=х-х 0 f(x) = f(x) – f(x 0 ) Предельное положение секущей при х 0 и называется касательной. Причем, Или

Сравните: По секрету: это и есть производная!

Определение: Производной функции y= f(x), заданной на интервале (a, b), в точке х этого интервала называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Итак, Ньютон, а затем Лейбниц, независимо друг от друга, пришли к открытию дифференциального и интегрального исчислений. Ньютон, а затем Лейбниц, независимо друг от друга, пришли к открытию дифференциального и интегрального исчислений.

Механический смысл производной: Производная пути по времени есть скорость Производная пути по времени есть скорость V(t) = S(t) V(t) = S(t)

Геометрический смысл производной: Тангенс угла наклона касательной, проведенной к кривой в точке х о, равен значению производной в этой точке. Тангенс угла наклона касательной, проведенной к кривой в точке х о, равен значению производной в этой точке. К кас. = f( х о ) К кас. = f( х о )

Тайны планетных орбит. Древнегреческие учёные умели решать немногие задачи кинематики – рассчитать либо равномерное прямолинейное движение, либо равномерное вращение вокруг оси. А планеты на небосводе двигались по самым замысловатым кривым . Свести эти движения планет к простым древним учёным не удавалось. Лишь в 17 веке немецкому учёному Иоганну Кеплеру удалось сформулировать законы движения планет. Оказалось, что планеты движутся по эллипсам, и притом неравномерно. Объяснить, почему это так, Кеплер не смог.

В конце 17 века Исаак Ньютон открыл законы динамики, сформулировал закон всемирного тяготения и развил математические методы, позволявшие сводить неравномерное к равномерному, неоднородное к однородному, криволинейное к прямолинейному. В основе лежала простая идея – движение любого тела за малый промежуток времени можно приближённо рассматривать как прямолинейное и равномерное. Одновременно с Ньютоном немецкий философ и математик Готфрид Вильгельм Лейбниц изучал, как проводить касательные к произвольным кривым.

Он также развил новое исчисление, которое оказалось по сути дела тождественным построенному Ньютоном. Обозначения, введённые Лейбницем, оказались настолько удачными, что сохранились и по сей день. Новая математика Ньютона и Лейбница состояла из двух больших частей – дифференциального и интегрального исчислений. В первом из них говорилось, как, изучая малую часть явления, сводить неравномерное к равномерному. Во второй – как из малых равномерных частей конструировать сложное неравномерное явление.

Дифференциальные исчисления – раздел математики, в котором изучаются производные и их применения к исследованию функции.

1). f(x) = 5x + 3 Найти : f(2) f(a) f(a+2) f(a+2) – f(a)

Приращение функции и аргумента х = х – х о – приращение аргумента  f (х) = f (х) – f (х о )  f (х) = f (х о + х ) – f (х о ) приращение функции – Найдите  f , если f ( х ) = х 2 , х о = 1, ∆ х = 0,5 Решение: f (х о ) = f (1) = 1 2 = 1, f (х о +  х ) = f (1 + 0,5) = f (1,5) = 1,5 2 = 2,25,  f = 2,25 – 1 = 1,25. Ответ:  f = 1,25 изменение

Calculis differentialis – исчисление разностей

Пусть точка движется вдоль прямой и за время t от начала движения проходит путь s(t). Рассмотрим промежуток времени от t до t+h , где h – малое число. Путь пройденный за это время s( t+h ) – s(t) .

Пусть функция f(x) определена на некотором промежутке, х – точка этого промежутка и число h ≠ 0 такое, что х+ h также принадлежит данному промежутку. Производной функции f(x) в точке х называется: приращение аргумента приращение функции

Исаак Ньютон (1643 – 1727) «Когда величина является максимальной или минимальной, в этот момент она не течет ни вперед, ни назад.» Механический смысл производной.

у = k х + в у(х о ) = k х о + в, у(х о + ∆х) = k ∙ (х о + ∆х) + в = k х о + + k ∆х + в, ∆у = у(х о + ∆х) – у(х о ) = k х о + k ∆х + + в – k х о – в = k ∆х, ( k х + в)′ = k Ответ: = k ∆х = k. ∆ x ∆ x ∆ y

Производная и её применение Урок алгебры в 11 классе

Вопрос 1 Сформулируйте определение производной функции в точке х 0.

Ответ Производная в данной точке есть предел отношения приращения f функции в точке х 0 к приращению x аргумента, когда последний стремится к нулю.

Вопрос 2 Какое условие является необходимым для существования производной функции в данной точке? Какое условие является необходимым для существования производной функции в данной точке? Верно ли обратное утверждение? Верно ли обратное утверждение?

Вопрос 3 Какую функцию называют дифференцируемой в точке x 0 ? Какую функцию называют дифференцируемой в точке x 0 ?

Ответ Функцией, дифференцируемой в данной точке считают функцию, имеющую производную в данной точке. Функцией, дифференцируемой в данной точке считают функцию, имеющую производную в данной точке.

Найди ошибку: 1) У = е х sin(x) У ‘ = (е х )’ sin'(x) = е х cos(x) У ‘ = (е х )’ sin'(x) = е х cos(x) 2) У = e 2x У ‘ = e 2x У ‘ = e 2x 3) У = cos(2-x) У ‘ =- sin(2-x) У ‘ =- sin(2-x)

У’ = е х sin(x) + e x cos(x) У’ = 2 е 2 х У’ = sin(2 – x)

Самостоятельная работа y e x – 4x e x + 3x 2 lnx + 5 x 6 – 4sinx 20x 4 – e x 2 x – e x log 5 x + e x 12x 3 – e x y x 2 + sinx 3 x – 5 x 2x 3 – x 2 + x x+ 3sinx lnx – 2cosx 9x 2 – cosx e x + 6x 2 2x 6 + 4sinx 175xx

Ключ к расшифровке высказывания yy’Буква окошка e x – 4x 2 + 7e x – 8xА15 e x + 3x 2 e x + 6xБ25 lnx + 5В1,12,16 x 6 – 4sinx6x 5 – 4cosxГ18 20x 4 – e x 80x 3 – e x Е2,7,9,13,17 2 x – e x 2 x lnx – e x И4,6,30,35 log 5 x + e x К14 12x 3 – e x 36x 2 – e x Л3,10,34 2x 6 + 4sinx12x 5 + 4cosxМ31

Ключ к расшифровке высказывания yy’Буква окошка 2x 6 + 4sinx12x 5 + 4cosxМ31 7x 5 – 20x 3 Н26 e x + 6x 2 e x + 12xО11,19,12,24,2 7 9x 2 – cosx18x + sinxП21 lnx – 2cosxТ29,36 x+ 3sinx1 + 3cosxС20,23,28,33 2x 3 – x 2 + x6x 2 – 2x + 1Ч5,8 3 x – 5 x 3 x ln3 – 5 x ln5Ы32 x 2 + sinx2x + cosxЬ37

Величие человека – в его способности мыслить. Блез Паскаль 1623 – 1662 французский математик, физик, философ

Вопрос 4 В чем состоит механический смысл производной? В чем состоит механический смысл производной?

Ответ Первая производная от закона движения тела есть закон изменения скорости данного тела Первая производная от закона движения тела есть закон изменения скорости данного тела Вторая производная от закона движения, или первая производная от закона изменения скорости есть ускорение данного тела Вторая производная от закона движения, или первая производная от закона изменения скорости есть ускорение данного тела

Вопрос 5 В чем состоит геометрический смысл производной? В чем состоит геометрический смысл производной?

Ответ Значение производной в данной точке есть угловой коэффициент касательной или тангенс угла наклона касательной к положительному направлению оси ОХ. Значение производной в данной точке есть угловой коэффициент касательной или тангенс угла наклона касательной к положительному направлению оси ОХ.

Точка движется прямолинейно по закону S (t) = t 3 – 2t 2 Выберите какой из формул задается скорость движения точки в момент времени t 1) 3t 2 – 2; 2) t 2 – 4t; 3) 3t 2 – 4t; 4) t 4 – 2t 3

Найдите угловой коэффициент, касательной, проведенной к графику функции f(x) = 7x –5lnx в его точке с абсциссой х 0 =1. 1) 1,4; 2)7; 3) 2; 4) 12.

Найдите тангенс угла наклона касательной, проведенной к графику функции f(x) = x 5 – 5x 2 – 3 в его точке с абсциссой х 0 = )15; 2)7; 3)11; 4) 12.

Понятие о производной функции, её геометрический и физический смысл. Уравнение касательной к графику функции

Цели урока: ОБУЧАЮЩАЯ : 1) Ввести определение производной функции на основе задач физики, рассматривая при этом физический смысл производной; 2) Выяснить геометрический смысл производной дифференцируемой функции; 3) Вывести уравнение касательной к графику функции, с использованием производной; 4) Научиться решать задачи на данную тему, используя полученные знания РАЗВИВАЮЩАЯ : 1) Способствовать развитию общения как метода научного познания, аналитико-синтетического мышления, смысловой памяти и произвольного внимания, 2) Развитие навыков исследовательской деятельности ВОСПИТАТЕЛЬНАЯ : 1) Способствовать развитию творческой деятельности 2) Развивать у учащихся коммуникативные компетенции, потребности к самообразованию.

S Время в пути равно t А B U=S / t

Предел приращения функции к приращению аргумента, если он существует, называют производной функции в точке x 0 и пишут:

Предельное положение секущей при стремлении точки M к A по кривой L, называют касательной к кривой L. y x0 x0x0 x f (x 0 ) f (x) M A B C y = f (x) Вспомним, что понимают под касательной к графику функции: L

Линейная функция и ее график Какой вид имеет линейная функция? y = kx+b – линейная функция. Что является графиком линейной функции? Графиком линейной функции является прямая. Число k называется угловым коэффициентом прямой. Угол α – углом между этой прямой и положительным направлением оси Ox.

y x 0 y = kx + b, k < 0 α б)б) Линейная функция и ее график

Геометрический смысл углового коэффициента прямой k: k = tg α a b c Вспомним определение тангенса – это отношение противолежащего катета к прилежащему. Т.е. tg α =b/a α

Геометрический смысл производной дифференцируемой функции y = f (x) y x0 Рис.2 y = f (x) x0x0 x 0 +h f (x 0 ) f (x 0 +h) M A h α α B С

y x0 Рис.3 x0x0 x 0 +h f (x 0 ) f (x 0 +h) M A h αB β f (x 0 +h) – f (x 0 ) C Геометрический смысл производной дифференцируемой функции y = f (x) y = f (x)

y x0 Рис.4 y = f (x) x0x0 x 0 +h f (x 0 ) f (x 0 +h) M A αB Геометрический смысл производной дифференцируемой функции y = f (x)

Геометрический смысл производной дифференцируемой функции y = f (x): Значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке.

Алгоритм нахождения производной функции

Домашнее задание Решить предложенные в карточках примеры, для домашнего изучения Башмаков М.И. «Математика», стр , составить опорный конспект

Мгновенная скорость и понятие производной

Итак, зная функцию, можно вычислить среднюю скорость ее изменения на любом промежутке. Но, когда автомобиль едет по шоссе, его спидометр показывает не среднее, а конкретное значение скорости в каждый момент времени. Другими словами, у автомобиля есть мгновенная скорость, и именно ее показывает спидометр. Как же узнать ее?

Например, пусть путь, пройденный машиной, задается функций s = t2. Нас интересует скорость автомобиля в момент t1 = 5 сек. Мы можем найти среднюю скорость на интервале от 5-ой до 6-ой секунды. Так, к пятой секунде машина успеет проехать 52 = 25 метров, а к шестой секунде она проедет 62 = 36 метров. Получится, что за промежуток ∆t, равный 6 – 5 = 1 секунде, машина проедет путь ∆s = 36 – 25 = 11 метров. Тогда средняя скорость на промежутке составит

Теперь возьмем более короткий промежуток ∆t, равный всего лишь 0,1 с. То есть мы рассмотрим период времени между моментом t1 = 5 cи t2 = 5,1 c. Снова-таки, к 5-ой секунде машина проедет 25 метров, а к моменту 5,1 сона пройдет 5,12 = 26,01 м. То есть за 0,1 с автомобиль преодолеет 26,01 – 25 – 1,01 м, а средняя скорость при этом составит

Ещё раз уменьшим промежуток ∆t. Пусть теперь он составляет всего 0,01с. Тогда средняя скорость будет определяться так:

Видно, что при уменьшении промежутка ∆t средняя скорость стремится к величине 10 м/с. Поэтому логично считать именно эту величину мгновенной скоростью машины в момент времени t = 5 c. Однако возникает вопрос – уверены ли мы, что мгновенная скорость стремится именно к 10 м/с, а не, скажем, к 10,001 м/с? Как точно определить это число? Здесь как раз помогают пределы. Можно записать, что мгновенная скорость – это предел отношения ∆s/∆t при ∆t, стремящемся к нулю. То есть

Получили, что мгновенная скорость в момент t1 = 5 действительно равна 10 м/с.

Задание. Вычислите мгновенную скорость разгоняющегося самолета через 10 секунд после начала разгона, если пройденное им расстояние задается законом s(t) = 5t2.

Решение. За 10 секунд самолет успеет преодолеть

Дадим функции s(t) приращение ∆t и обозначим как t1 момент времени, когда со старта прошло 10 секунд. Тогда к моменту t1 + ∆t самолет успеет пройти

Решая данную задачу, мы дали функции s(t) приращение ∆t и записали отношение ∆s/∆t. Далее мы устремили величину ∆t к нулю и посмотрели, к какому числу устремится отношение ∆s/∆t. Это число и оказалось мгновенной скоростью. В более общем случае произвольной функции у = f(x)в точке х0 можно дать приращение аргумента ∆х, которому будет соответствовать некоторое приращение функции ∆у. Далее можно вычислить предел отношения ∆у/∆х, который будет характеризовать, как быстро в точке х0 функция меняет свое значение. Этот предел называют производной функции в точке х0. Для обозначения производной над функцией ставят штрих.

В общем случае алгоритм вычисления производной в некоторой точке следующий:

1.Фиксируем точку х0, вычисляем для нее значение функции у(х). Это значение будет конкретным числом

• Даем функции приращение аргумента ∆х, переходим в новую точку х0 + ∆х, вычисляем в ней значение функции у(х0 + ∆х). Это значение будет не числом, а выражением, содержащим переменную ∆х.
• Находим приращение функции ∆у, используя формулу

Это приращение также должно содержать величину ∆х.

Задание. Найдите производную функции у = 4х2 + 7х в точке х0 = 2.

Решение. Сначала вычислим значение функции в точке х0:

Далее определяем величину у(х0 + ∆х) (это будет не конкретное число, а некоторое выражение, содержащее переменную ∆х):

Задание. Найдите производную функции у = 1/х в точке х0 = 5.

Решение. Высчитаем у(х0):

Пусть у функции есть приращение ∆х, тогда в точке х0 + ∆х ее значение составит:

В рассмотренных примерах для вычисления производной мы использовали ее определение. Однако на практике такой метод почти не используется. В будущем мы узнаем более эффективные способы для нахождения производной.

Мы уже убедились, что использование производной помогает находить мгновенную скорость тел. По этой причине понятие производной функции играет огромную роль в механике (разделе физике, изучающем движение). Однако этим ее практическое применение не ограничивается. По сути, она является основой для всей классической физики, и именно ее появление в XVII в. обеспечило выдающийся прогресс в науке вплоть до конца XIX в. При этом производная используется и в геометрии для анализа графиков функций. Более подробно ее применение будет также рассмотрено позже.

Физический смысл производной

Вводя понятие производной, мы предварительно решали задачи на поиск мгновенной скорости некоторого тела (автомобиля, пешехода, самолета). Во всех них в качестве исходных данных задавался некоторый закон, который описывал зависимость пути, пройденного телом, от времени. Обычно этот закон представлял собой функцию s(t). Для нахождения мгновенной скорости мы сначала записывали выражение для вычисления средней скорости, которое содержало переменную величину ∆t. На следующем шаге мы составляли выражение ∆s/∆t, после чего величину ∆t мы устремляли к нулю и смотрели, чему в таком случае будет равняться предел отношения ∆s/∆t. Этот предел и принимался за мгновенную скорость тела.

Можно заметить, что последовательность наших действий совпадает с теми действиями, которые выполняются для вычисления производной. Разница лишь в обозначениях. В случае с производной мы рассматриваем функцию у(х), а в случае с поиском скорости тела – функцию s(t). Но если поменять букву t на х, а s на t, то окажется, что поиск мгновенной скорости в момент времени t0 – это тоже самое, что и поиск производной функции s(t) в точке t0. Таким образом, можно сформулировать физический смысл производной (иногда его называют механическим смыслом, так как в физике производная используется не только в механике):

Функцию s(t) обычно называют законом движения. Рассмотрим простейший случай, когда тело движется с постоянной скоростью, равной, например, 3 м/с. Из физики известно, что в таком случае путь s, пройденный телом за время t, можно вычислить по формуле

где v – скорость.

Значит, закон движения тела будет выглядеть так:

Найдем производную в произвольный момент времени t0. Так как производная должна совпадать со скоростью, то независимо от значения t0 производная должная оказаться равной 3. Действительно, в точке t0 значение функции равно

Дадим приращение аргумента ∆t. В точке t0 + ∆t функция будет равна

Найдем приращение функции ∆s:

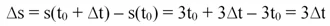
Обратите внимание – величина ∆s уже не зависит от t0. Далее найдем отношение ∆s/∆t:

Действительно, получилось, что производная s′(t) в любой точке равна 3, то есть она совпадает со скоростью.

Предел функции на бесконечности

Рассмотрим довольно простую функцию

y = 1/x

Её график называется гиперболой и выглядит так:

Можно заметить, что при больших положительных значениях х график функции приближается к горизонтальной оси Ох, но не пересекает её. Действительно, если мы будем вычислять значение у при всё больших значениях х, то будем получать всё меньшие, но всё же положительные числа:

Получается, что при бесконечном росте аргумента х функция стремится к нулю. Можно ли эту особенность функции как-то записать, используя математические символы? Оказывается, можно, и выглядит это запись так:

которая означает, что х стремится к бесконечности. После символа lim записана сама функция 1/х. В целом вся запись читается так: «предел функции у = 1/х при х, стремящемся к бесконечности, равен нулю».

Вернемся к графику функции у = 1/х. Видно, что если мы будем брать всё меньшие отрицательные значения х, то функция также будет стремится к нулю. Действительно, попробуем подставлять в нее как можно меньшие значения аргумента:

Чтобы записать эту особенность функции, используется следующая запись:

который может быть получен параллельным переносом графика у = 1/х на две единицы вверх:

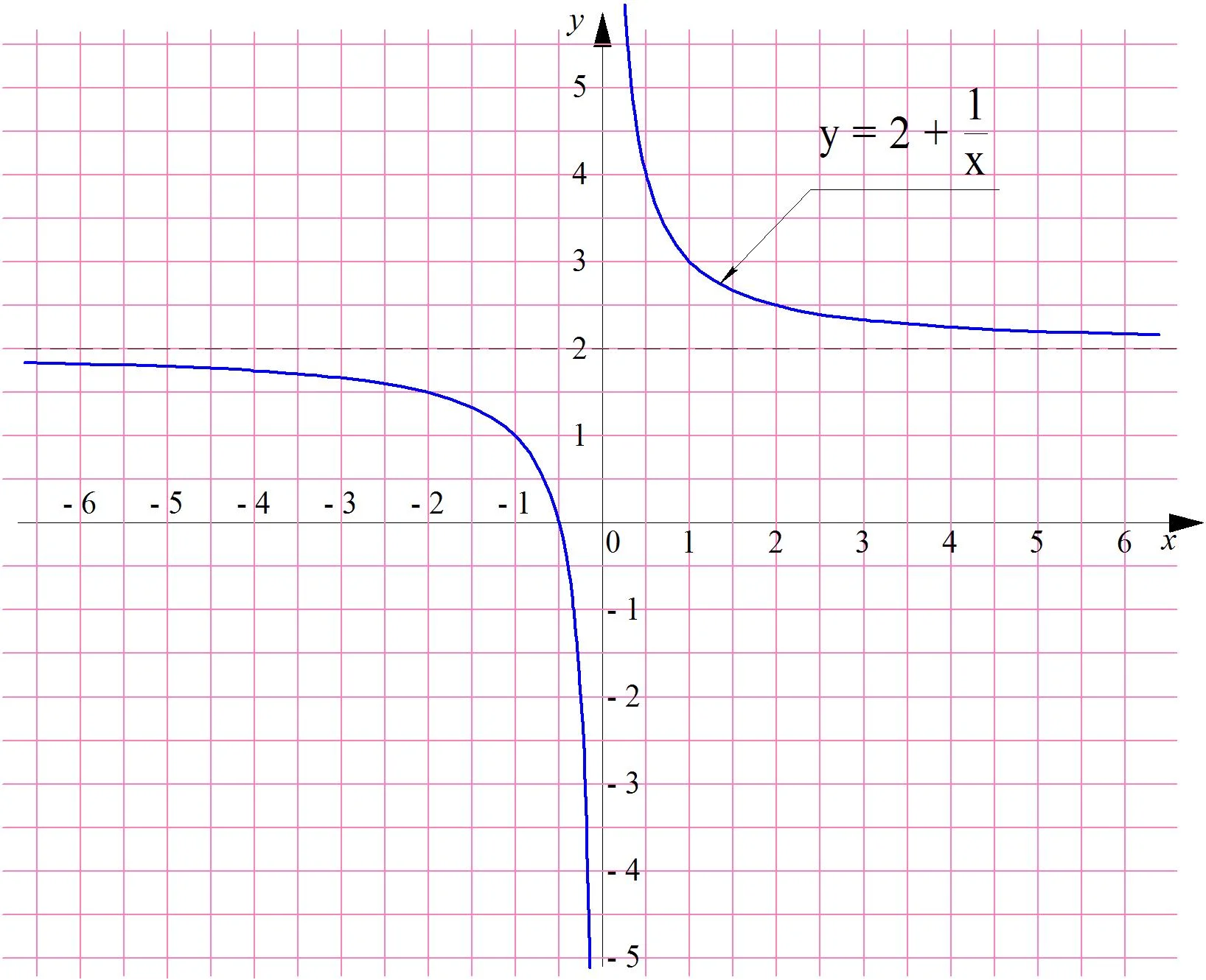
Возможны случаи, когда при бесконечном увеличении аргумента функции она не стремится к какому-то конкретному числу, а сама также неограниченно возрастает. Для примера посмотрим на график у = х3:

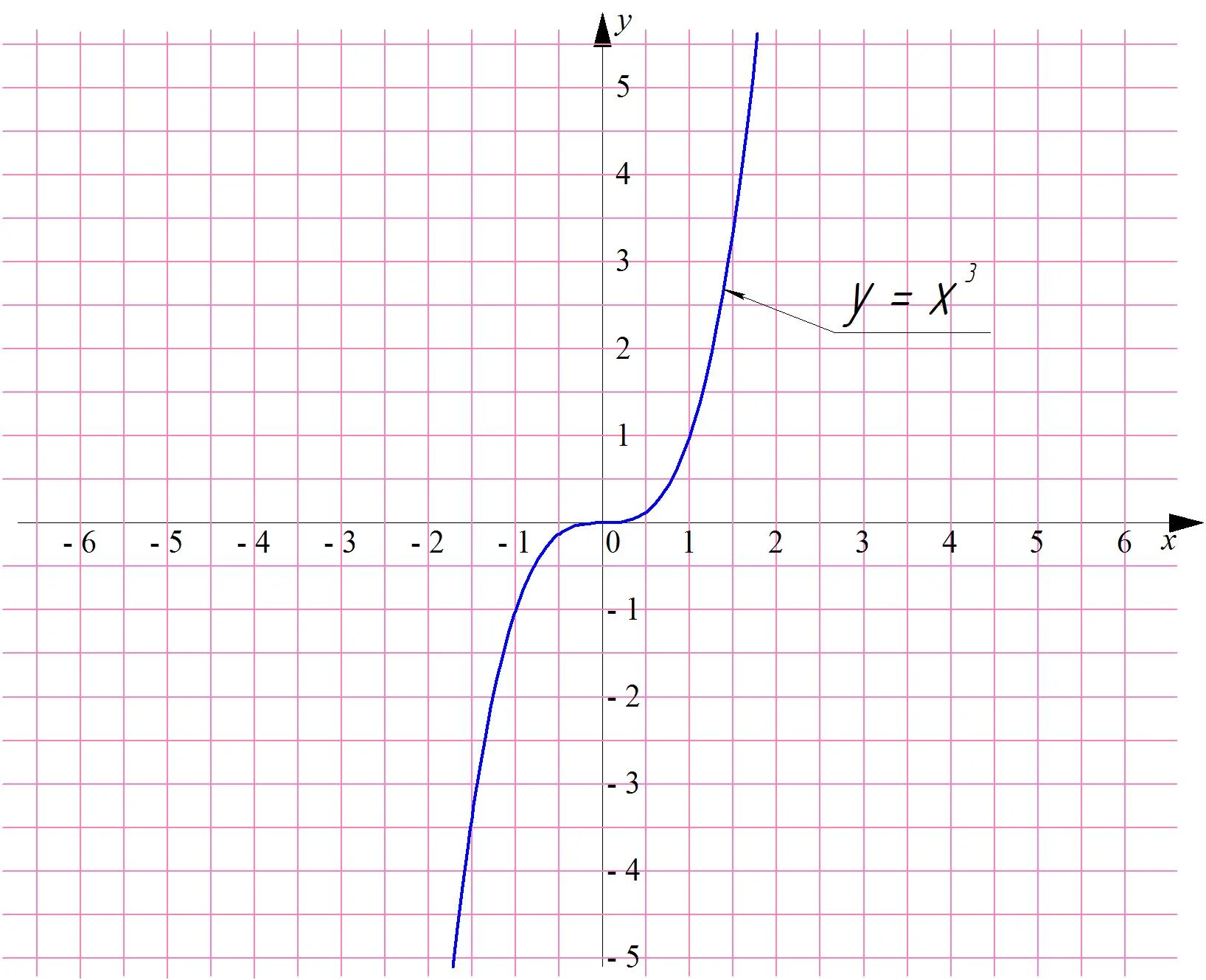
Возникает вопрос – для всякой ли функции можно указать ее предел на бесконечности? Оказывается, что нет. Для примера рассмотрим тригонометрическую функцию у = sinx, графиком которой является синусоида:

С одной стороны, sinx явно не стремится к какому-то конкретному числу при увеличении х, он «колеблется» между числами 1 и (– 1). С другой стороны, нельзя и сказать, что он стремится к бесконечности. Получается, что у этой функции просто нет пределов на бесконечности.

Производная сложной функции

«Сконструировать» громоздкую функцию из нескольких простых можно не только с помощью арифметических действий. Например, возьмем функции

В обоих случаях мы получили некоторую функцию, продифференцировать которую с помощью уже известных нам правил не получится. Функции, сконструированные таким образом, называются сложными. Есть универсальная формула, позволяющая находить производную сложной функции:

Посмотрим, как пользоваться эти правилом. Пусть надо вычислить производную функции

Она сконструирована из функции у = ex и у = sinx, причем вторая подставлена в первую. Это значит, что первую можно обозначить буквой u, а вторую – буквой v (если использовать обозначения в правиле 5):

Задание. Найдите у′, если у = sin 2x.

Решение. На этот раз в качестве исходной функции выступает

Убедиться в справедливости правила 5 можно на примере функции

Её можно продифференцировать двумя разными способами. Сначала попробуем просто избавиться от квадрата в исходной функции, используя формулу квадрата суммы:

В результате оба способа вычисления производной дали одинаковый ответ.

Решение. В данном случае мы рассматриваем комбинацию следующих функций:

Теперь мы умеем вычислять производные почти любых функций, которые можно записать с помощью элементарных функций и арифметических операций. При этом нам не надо использовать определение понятия производной и вычислять какие бы то ни было пределы. Достаточно знать производные основных функций и несколько (всего лишь 5) правил дифференцирования. Навыки дифференцирования функций пригодятся в будущем при решении практических задач, связанных с производными.

Производная как функция

До этого мы вычисляли значение производной в отдельных точках графика. Она представляет некоторое число у′(х0). Однако чаще всего производную можно вычислить в каждой точке графика у(х). То есть каждой точке х0 соответствует какое-то число у′(х0). Но если есть соответствие между числами х0 или у′(х0), то можно говорить о функции. Её обозначают как у′(х), или просто как у′.

Объясним, чем отличаются обозначения у′(х0) и у′. Обе эти величины называются производными и вычисляются для некоторой функции у(х). Однако у′(х0) – это конкретное значение производной, то есть число. Например, 4 или 6. А выражение у′(х) – это не число, а функция, например, у = сили у = х3. Подставив в выражение у′(х) значение х0, можно узнать и у′(х0).

Возникает вопрос – а как находить функцию у′(х)? Для этого можно использовать определение производной, как и в случае су′(х0). Только вместо значения х0 не требуется подставлять какое-то число. Продемонстрируем эту процедуру на примере.

Пусть есть функция у = х2. Найдем у′(х). Для этого дадим произвольной точке с координатой х приращение х. В результате попадем в новую точку (х + х). Вычислим значения функции у = х2 в точках х и (х + х):

Далее находим величину у:

шаг – вычисляем отношение

Получили, что у′ = 2х. Ещё раз обратите внимание, что у′– это функция, а не число. Поиск производной называют операцией дифференцирования. Для краткости иногда используют такую запись:

Здесь в левой части в скобках записана исходная функция. Над скобкой стоит штрих, который и означает дифференцирование. Справа записана производная. Когда надо вычислить производную, используют такие фразы, как «продифференцируем функцию» или «возьмем производную».

Итак, мы получили, что (х2)′ = 2. Эту формулу производной для функции у =х2 стоит запомнить.

Скажем сразу, что пока мы будем в основном рассматривать примеры, где необходимо продифференцировать функцию у = х2, так как ее производная имеет простой вид и уже найдена нами. В следующих уроках мы научимся дифференцировать другие, значительно более сложные функции.

Найдя у′, мы существенно упрощаем свою жизнь. Пусть нам надо найти значение производной функции сразу в 5 точках. Раньше мы бы для каждой точке давали бы приращение , искали соответствующее ему значение у, вычисляли бы отношение у/х, а потом находили бы предел этого отношения. То есть нам надо было бы вычислить сразу 5 пределов. Однако зная у′, мы можем просто подставлять в неё значение х0 и сразу находить производную.

Задание. Найдите производную функции у = х2 в точке х0 = 100.

Решение. Известно, что (х2)′ = 2, то есть для функции у = х2 производная равна

Подставим значение х0 = 100 в производную:

Задание. К графику у = х2 в точках х1 = 0,5 и х2 = – 0,5 проведены касательные. Под каким углом пересекаются эти касательные?

Чтобы найти угол между двумя касательными, сначала найдем, какие углы они образуют с горизонтальной линией Ох. Для этого вычислим производную от у = х2 в точках 0,5 и (– 0,5). Так как у′ = 2х, то

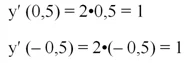
Получается, что тангенс наклона 1-ой касательной равен единице, это значит, что сам угол равен 45°. Тангенс наклона второй касательной равен (– 1). Чтобы найти угол ее наклона, составим тригонометрическое уравнение:

Естественно, уравнение имеет бесконечно большое количество решений: – π/4; 3π/4; 7π4 и т.д. Среди них нас интересует то, которое соответствует углу от 0 до 180°. Это угол 3π/4, который равен 135°.

Итак, касательные имеют углы наклона, равные 45° и 135°. Далее поиск угла их пересечения становится простой и чисто геометрической задачей. Добавим точки на рисунок:

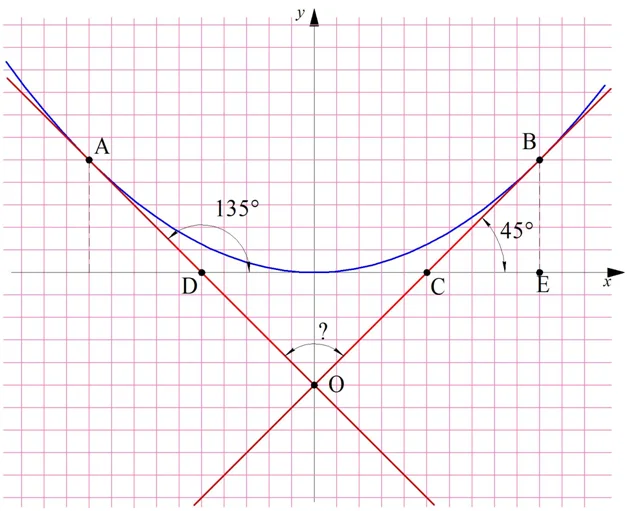
Мы нашли, что ВСЕ = 45° и А = 135°. Тогда

Тогда из треугольника можно найти и интересующий нас . Мы используем тот факт, что сумма углов любого треугольника составляет в точности 180°:

В итоге получаем, что прямые пересекаются под прямым углом.

Задание. Автомобиль стартует и набирает скорость, при этом закон его движения имеет вид () = 2. Найдите скорость машины через 2,3, 4 и 5 секунд после старта. Постройте график, иллюстрирующий зависимость скорости машины от времени.

Решение. Скорость машины будет равна производной ее закона движения. Производная функции () = 2 имеет вид ′() = 2. Подставляя в производную значения 2, 3, 4 и 5, найдем скорость автомобиля в эти моменты времени:

Так как ′() = 2, а скорость равна производной, то есть () = ′(), то получаем, что зависимость скорости от времени имеет вид () = 2. Её график будет выглядеть так (на нем отмечены те самые точки, которые соответствуют 2, 3, 4 и 5 секунде после старта):

Ответ: 4, 6, 8 и 10 м/с.

Рассмотренный пример показывает, что зная закон движения (), можно не просто вычислить скорость тела в отдельные моменты времени, но и получить зависимость, то есть общую формулу, позволяющую вычислять скорость. Другими словами, график производной ′() совпадает с графиком скорости ()

Связь производной с возрастанием и убыванием функций

Заметим, что если провести касательную к графику в той точке, где функция возрастает, то сама эта касательная окажется также возрастающей линейной функцией. При этом угол ее наклона будет острым:

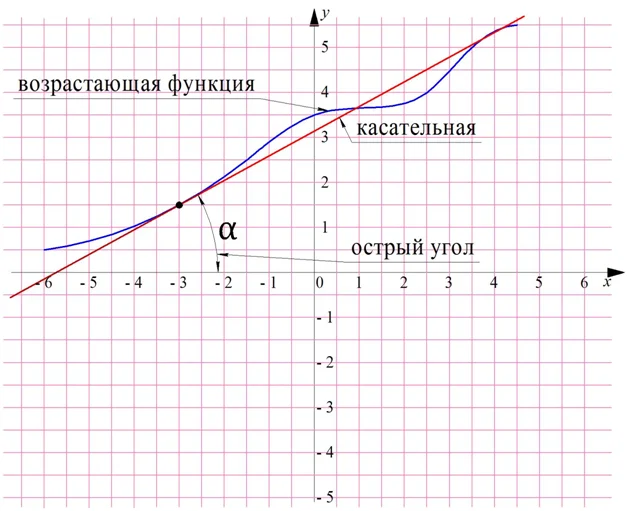
Однако это тангенс равен значению производной. Значит, она также положительна, если функция возрастает.

Ситуация меняется в случае убывающей функции. Тогда и касательная к графику оказывает убывающей линейной функцией. Из-за этого она образует с горизонтальной осью Ох не острый, а тупой угол:

Напомним, что тангенс тупого угла является отрицательным числом. Но тогда и производная должна быть отрицательная. Получается, что по знаку производной можно определить, убывает или возрастает функция в данной точке.

Задание. Определите знак производной функции у = в точке х0 = 3π/4, не вычисляя её.

Решение. График у =выглядит так:

Точка х0 = 3π/4 находится между π/2 и π. Видно, что в этой точке функция убывает. Следовательно, производная в этой точке отрицательна.

Ответ: Производная отрицательна.

Производные некоторых элементарных функций

Нам известно несколько основных функций, которые в математике чаще называют элементарными. Например, элементарными являются линейная функция, степенная, показательная, логарифмическая. Также существует несколько различных тригонометрических функций (синус, косинус, тангенс), которые тоже считаются элементарными. Попытаемся вычислить для них производные.

Начнем с линейной функции. В общем случае она выглядит так:

где k и b – некоторые постоянные числа.

Выберем произвольную точку х0 и дадим ей приращение ∆х, в результате чего мы придем в новую точку (х0 + ∆х). Вычислим значения линейной функции в этих двух точках:

Теперь мы можем найти приращение функции ∆у:

Находим отношение ∆у/∆х:

Задание. Вычислите производную функции у = 4х + 9.

Обратите внимание, что в рассмотренном примере запись у′ = 4 означает функцию. Просто при любом значении х она принимает одно и то же значение, равное 4. График производной функции будет выглядеть так:

Рассмотрим два особых частных случая линейной функции. Пусть k = 1 и b = 0, тогда она примет вид у = х. Её производная тогда будет равна 1:

Теперь предположим, что коэффициент k = 0. Тогда функция примет вид

где С – некоторое постоянное число, то есть константа (большая буква Св таких случаях используется из-за латинского термина constanta). Производная такой функции будет равна нулю:

Задание. Найдите вторую производную функции у = 9х + 2.

Решение. Сначала вычислим первую производную:

Очень легко объяснить, почему производная константы равна нулю. Представим себе, что закон движения некоторого тела выглядит как s(t) = C, например, s(t) = 5. Это значит, что тело в любой момент времени находится в точке, находящейся в 5 метрах от какого-то начала отсчета. То есть тело находится в одной и той же точке, а это значит, что оно не двигается. Тогда его скорость равна нулю. Но производная – это и есть скорость, значит, она также равна нулю.

Далее вычислим производную для функции у = 1/х. Выберем некоторую точку х0 и дадим ей приращение ∆х. В результате имеем две точки с координатами х0 и (х0 + ∆х). Вычислим значение функции в каждой из них:

Задание. Вычислите производные функции

Обратите внимание, что производная функции у = 1/х оказывается отрицательной при любом значении х (кроме нуля, для которого производную посчитать нельзя, так как получится деление на ноль). Это должно означать, что функция убывает в каждой своей точке, а любая касательная к ней образует с осью Ох тупой угол наклона. И это действительно так:

Мы разобрали несколько простейших примеров того, как находить формулы производных. Для этого используется понятие предела функции. Для вывода всех подобных формул требуется хорошо знать тему вычисления пределов, которая не изучается детально в школе. Поэтому мы просто дадим следующие формулы без доказательств.

Начнем со степенной функции у = хn, где n– некоторое постоянное число. Её производная вычисляется по формуле:

Приведем примеры использования этой формулы:

Задание. Найдите производную функции у = х6 в точке х0 = 10.

Задание. Движение самолета при разгоне описывается законом движения s(t) = t3. Найдите его скорость через 5 секунд после начала разгона.

Решение. Скорость самолета в любой момент времени равна производнойs′(t). Найдем её:

Заметим, что используемая нами формула работает и в том случае, если показатель степени является отрицательным или дробным числом. Действительно, ранее мы вывели формулу

По определению отрицательной степени мы можем записать, что

Задание. Определите, в какой точке необходимо провести касательную к графику функции

чтобы она образовывала с осью Ох угол в 45°?

Решение. Тангенс угла наклона касательной равен производной. Известно, что tg 45° = 1. Значит, нам надо найти такую точку х0, в которой значение производной квадратного корня будет равно единице. Производная вычисляется по формуле:

Ответ: х0 = 0,25.

Далее изучим формулы производных для тригонометрических функций. Они выглядят так:

Рассмотрим несколько примеров использования этих формул.

Задание. Найдите производную функции у = cosx в точке х0 = π.

Решение. Мы знаем, что

Задание. Найдите угол наклона касательной, проведенной к графику у = sinx в начале координат.

Решение. Производная синуса вычисляется по формуле:

Получается, что тангенс угла наклона также равен единице. Это значит, что сам угол равен 45°. Построение показывает, что это действительно так:

Задание. Найдите производную функции у = tgx в точке х0 = π/6.

Решение. Для тангенса используется формула:

Далее рассмотрим показательную и логарифмическую функцию. Их производные рассчитываются по следующим формулам:

Обратите внимание, что в этих формулах появился натуральный логарифм, то есть логарифм, основанием которого является число е. Именно из-за наличия натурального логарифма в формулах дифференцирования он играет особо важную роль в математике и имеет отдельное обозначение. Вычислим несколько производных с помощью приведенных формул:

Напомним, что справедлива формула

Стоит обратить внимание, что функции у = ех при дифференцировании не меняется. Эта особенность функции также имеет огромное значение в математическом анализе.

Задание. Найдите угол наклона касательных, проведенных к графику у = ех в точке (0; 1) и к графику у = lnx в точке (1; 0).

Решение. Используем формулы производных:

Получили, что тангенс наклона касательной равен 1. Из этого следует, что угол наклона касательной равен 45°. Далее найдем производную натурального логарифма при х = 1:

Производная снова равна 1, значит, угол наклона также составит 45°, что подтверждается рисунком:

Задание. Вычислите производную функции у = 2х при х0 = 3.

Решение. Используем формулу

Сведем использованные нами равенства в одну таблицу производных основных функций:

Приращение аргумента и функции

Часто нас интересует, как изменяется функция при изменении аргумента. Например, известно, что объем куба вычисляется по формуле

где а – ребро куба. Предположим, что мы провели измерения какого-то куба и выяснили, что длина его ребра равна 2 см. Тогда объем куба составит 23 = 8 см3. Но ведь любое измерение производится не с абсолютной точностью, а с некоторой погрешностью. Как оценить погрешность вычисления объема, если известна погрешность измерения его ребра?

Пусть с учетом погрешности линейки, составляющей 0,1 см, известно, что длина ребра находится в диапазоне от 2 до 2 + 0,1 = 2,1 см. Тогда максимально возможный объем куба составит 2,13 = 9,261 см3. Получается, что погрешность в измерении объема куба составляет 9,261 – 8 = 1,261 см3.

С точки зрения математического анализа мы в данном случае рассматривали поведение функции у = х3 в точке х = 2. Мы допустили некоторое изменение величины х, которое называют приращением аргумента и обозначают как ∆х. Далее мы высчитали, какое изменение величины у, или приращение функции, обозначаемое как ∆у, соответствует этому приращению аргумента. Выяснилось, что приращению ∆х = 0,1 соответствует приращение ∆у = 1,261.

В более общем случае произвольной функции у = f(x) можно дать некоторое приращение ∆х в некоторой точке х0. В результате этого изменится и само значение f(x), причем величину этого изменения обозначают как ∆у. Это можно проиллюстрировать графически:

Задание. Дана функция у = 3х2 + х + 4. Вычислите приращение функции в точке х0 = 5, если ∆х = 1.

Решение. Сначала вычислим новое значение аргумента функции, с учетом данного ему приращения:

Далее вычислим значения функции, соответствующие старому и новому аргументу:

Задание. Радиус круга, измеренный с погрешностью не более 0,5 см в меньшую сторону, равен 10 см. Оцените погрешность вычисления его площади.

Решение. Площадь круга рассчитывается по формуле:

Правила нахождения производных

Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.

Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

Для наших читателей сейчас действует скидка 10% на любой вид работы

Выносим константу

Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте.

Пример. Вычислим производную:

Производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

Производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Производная частного двух функций

Формула для определения производной от частного двух функций:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

Геометрический смысл производной

Возьмем график произвольной функции у(х) и выберем на ней точку х0 (обозначим ее как А). Дадим ей приращение ∆х. Тогда мы получим новую точку с абсциссой х0 + ∆х, которую обозначим буквой В. Соединим исходную и новую точку прямой линией АВ. Эта линия пересекает график как минимум в двух точках (А и B), поэтому мы можем назвать её секущей. Проведем также касательную к графику функции в точке А:

Если из точки B провести вертикальную линию, а из точки А – горизонтальную, то они пересекутся в некоторой точке О. Рассмотрим треугольник АОВ. Очевидно, что он прямоугольный (∠ АОВ = 90°). При этом АО = ∆х, а ОВ = ∆у. Так как АО и ОВ – это катеты прямоугольного треугольника, то их отношение (ОВ/АО) равно тангенсу угла ВАО, который на рисунке обозначен как α:

Ещё раз отметим, что угол α – это угол между секущей и горизонтальной линией. Этот угол определяется именно отношением величин ∆у и ∆х.

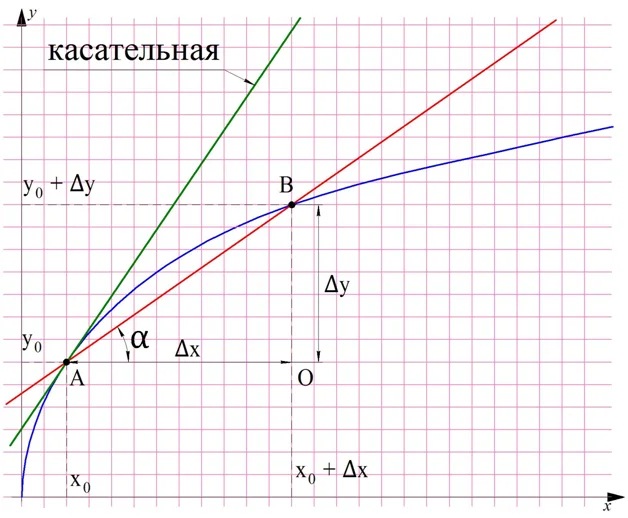
Мы видим что при уменьшении ∆х секущая АВ приближается к касательной. В конце концов, при «максимальном» уменьшении ∆х, Точка В почти сольется с точкой А, а секущая АВ почти сольется с касательной. Тогда и угол α, являющийся углом наклона секущей, будет почти не отличаться (или отличаться на бесконечно малую величину) от угла наклона касательной. Поэтому можно принять, что угол α – это и есть угол наклона касательной:

Но мы уже определили ранее, что тангенс угла α – это отношение ∆у/∆х:

Получается, что в предельном случае, когда ∆х стремится к нулю, секущая, по сути, становится касательной к графику, а отношение ∆у/∆х – производной (по ее определению):

Отсюда следует, что значение производной в точке х0 совпадает с тангенсом угла наклона касательной к графику функции в этой же точке. В этом заключается геометрический смысл производной.

Здесь следует уточнить понятие касательной. Из геометрии известно понятие касательной к окружности. Так называют прямую, имеющую с окружностью ровно одну общую точку. Однако для касательной к графику функции такое определение не подходит. Действительно, любая строго вертикальная прямая пересечет график функции только в одной точке, однако назвать ее касательной нельзя, ведь она проходит «сквозь график»:

С другой стороны, прямая, касающаяся графика в одной точке, может потом пересечь его в другой точке:

Поэтому касательную к графику в точке х0 определяют именно как предельное положение секущей, которое получается, когда промежуток ∆х устремляют к нулю.

Решение. Тангенс искомого угла можно найти, вычислив производную. Для этого сначала вычислим значение функции в точке х0:

Теперь даем приращение ∆х и вычисляем функцию в точке (х0 + ∆х):

Далее находим величину ∆у, то есть приращение функции в точке х0:

Отношение ∆у/∆х можно определить так:

Если устремить величину ∆х к нулю, то отношение ∆у/∆х устремится к единице:

Значит, и производная в точке х0 = 2 будет равна 1:

Производная – это тангенс угла наклона касательной, то есть

Так как тангенс 45° равен единице, то α = 45°. Убедимся в этом, проведя через точку (2; 1) прямую с таким наклоном. Она действительно оказывается касательной:

Вторая производная функции и ее физический смысл

Итак, мы узнали, что при дифференцировании функции мы получаем какую-то новую функцию. Встает логичный вопрос – а можно ли продифференцировать и эту новую функцию? Естественно можно, и в результате получат ещё одну функцию, которую называют второй производной. Для ее обозначения используют уже не один штрих, а сразу два: у′′. При необходимости можно взять и третью производную (у′′′), и четвертую (у′′′′), и даже сотую или тысячную. Однако при рассмотрении большинства практических задач достаточно первых двух производных.

Есть ли у второй производной функции физический смысл? Да. Дело в том, что в физике различают равномерное и ускоренное движение тела. В первом случае оно двигается с постоянной скоростью, а во втором скорость тела может изменяться. В связи с этим вводится и такая физическая величина, как ускорение. Она характеризует то, как быстро изменяется скорость тела. То есть ускорение – это скорость изменения скорости. Для обозначения ускорения обычно используют букву а. И для определения ускорения как раз и может потребоваться вторая производная.

Действительно, если ускорение – это скорость изменения скорости, то ее можно найти, взяв производную от функции (), то есть а() = ′(). Однако сама скорость получается при дифференцировании закона движения (), то есть () = ′(). Тогда получается, что

То есть физический смысл второй производной заключается в том, что вторая производная закона движения ′′() в момент 0 равна ускорению тела в этот самый момент.

Ещё раз взглянем на пример, который мы уже рассмотрели. Пусть автомобиль стартует с места, и пройденный им путь определяется законом () = 2. Мы уже выяснили, что в этом случае его скорость можно рассчитать по формуле () = 2. Получается, что скорость тела непостоянна, значит, имеет место ускоренное движение. Попробуем найти величину ускорения.

Для этого возьмем производную от функции () = 2. Возьмем какое-то значение аргумента и дадим ему приращение , в результате получим новый аргумент ( + ). Вычислим скорость тела в эти моменты времени:

Теперь мы можем найти приращение функции , соответствующее приращению

Далее находим отношение /:

Получили, что это отношение является постоянной величиной и равно 2. Естественно, что предел постоянной величины равен этой величине:

Итак, получили, что производная ′ – это постоянное число, не зависящее от времени. Оно же равно ускорению тела. Значит, в любой момент времени ускорение тела равно 2м/с2.

Напомним, что важнейший закон механики, известный как второй закон Ньютона, выглядит так:

где – это сила, действующая на тело;

а – ускорение.

Однако теперь мы знаем, что ускорение является второй производной от закона движения. В связи с этим его можно переписать в виде

И на самом деле в физике значительно чаще используется именно такая его формулировка. Это лишний раз подтверждает значимость понятия производной.

Геометрический и физический смысл производной

Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.

Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

Средняя скорость изменения функции

Часто в физике и других естественнонаучных дисциплинах одни величины характеризуют изменение других величин. Классический случай – это скорость, которая характеризует, насколько быстро изменилось положение тела (или материальной точки в пространстве). Рассмотрим пример. Пусть пешеход движется по прямой улице с постоянной скоростью 2 м/с. Попытаемся построить график, который иллюстрирует зависимость пройденного пешеходом пути и его скорости от времени. Известно, что при равномерном прямолинейном движении пройденный путь можно найти по формуле:

S = v*t

Где s – путь;

V – скорость;

t – время.

Так как скорость равна 2 м/с, то зависимость пути от времени будет выглядеть так:

s(t) = 2t

которая является прямой пропорциональностью. Поэтому ее график будет прямой линией:

Так как скорость во время всего движения остается равной 2 м/с, то зависимость скорости от времени будет иметь вид v = 2, а выглядеть она будет как горизонтальная линия:

В данном случае найти зависимости s(t) и v(t) было очень легко. Но теперь усложним задачу. Пусть зависимость s(t) задается не прямой линией, а некоторой кривой:

Можно ли теперь что-то сказать о скорости движения пешехода?

Ясно, что в различные моменты времени скорость пешехода различна. Но мы можем найти среднюю скорость пешехода в какой-то момент времени. Например, рассмотрим промежуток времени со 2-ой по 10-ую секунду.

Его протяженность, очевидно, равна 10 – 2 = 8 секундам. Если первый момент времени обозначить как t1, а второй как t2, то протяженность этого промежутка времени (∆t) можно вычислить по формуле

Судя по графику, к моменту времени t1 пешеход прошел только 1 метр, а на момент t2он преодолел уже 9,5 м. Сколько же метров он прошел за промежуток времени ∆t? Если первое расстояние обозначить как s1, а второе как s2, то пройденное расстояние (∆s) можно рассчитать так:

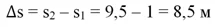
Тогда средняя скорость на рассматриваемом участке можно вычислить, поделив ∆s на ∆t

В данной ситуации мы рассматривали функцию, которая задает зависимость между перемещением пешехода и временем. Средняя скорость характеризует, как быстро двигается пешеход, то есть как быстро функция s(t) меняет своё значение. Очевидно, что в данном случае величина ∆t – это некоторое приращение аргумента функции s(t), в то время как ∆s– это приращение самой функции. Получается, что с помощью приращений можно вычислять среднюю скорость объектов.

Однако в физике рассматривается не только скорость перемещения вточек пространстве. Например, можно говорить о скорости остывания горячего чайника. Пусть его температура меняется по закону, график которого представлен на рисунке:

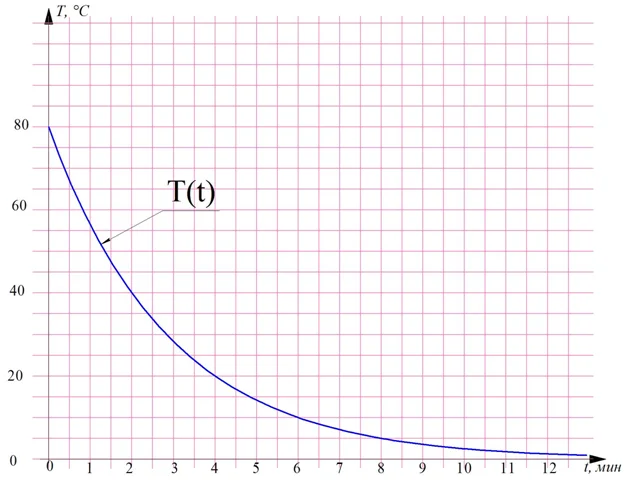
Можно ли узнать, с какой средней скоростью остывал чайник на промежутках от 2-ой до 4-ой минуты? Да, для этого надо в точке t = 2 мин дать приращение аргумента ∆t = 2мин и посмотреть, какое приращение ∆T получит сама функция:

Пусть t1 = 2 мин, а t2 = 4 мин. Тогда

По графику видно, что в момент t1 температура чайника составляет Т1 = 40°С. Через две минуты она уже упала до отметки Т2 = 20°С. Получается, что за промежуток ∆t функция T(t) получила приращение

Обратите внимание, что приращение оказалось отрицательным. Дело в том, что температура чайника падала, то изменялась в меньшую сторону. Знак минус указывает именно на направление изменения функции. Если бы чайник нагревался, то приращение оказалось бы положительным.

Теперь мы можем вычислить среднюю скорость остывания чайника на промежутке между 2-ой и 4-ой минутой:

Знак минус указывает на то, что температура на этом промежутке времени уменьшается, а не возрастает.

В более общем случае, когда у нас есть произвольная функция у = f(x), с помощью приращений можно вычислить среднюю скорость её изменения на каком-нибудь промежутке. Пусть первая точка промежутка обозначается как х0, а его протяженность составляет ∆х. Тогда первой точке соответствует значение функции у(x0), а концу промежутка – значение у(x0 + ∆x):

Предел функции в точке

Порою нас интересует поведение функции не на бесконечности, а вблизи конкретной точки х0. Конечно, в большинстве случае можно просто вычислить функцию в этой точке, однако иногда это невозможно сделать. Для примера рассмотрим функцию

Очевидно, что точка х = 2 не входит в ее область определения, ведь при подстановке этого значения в функцию знаменатель дроби обратится в ноль. Однако в любой другой точке значение функции будет равняться единице:

График такой функции будет выглядеть как прямая у = 1, у которой есть одна «выколотая точка», соответствующая х = 2:

Итак, функция не определена в точке х = 2, однако можно вычислить предел функции в точке х = 2. Действительно, при любом, сколь угодно близком к 2 значении х функция будет равна единице:

Попробуем также приблизиться к точке 2 с другой стороны, подставляя в функцию числа, меньшие двух:

Снова всё время получается единица. Поэтому мы можем уверенно записать, что

Значительно чаще приходится иметь дело с пределами в точке, которые равны бесконечности. Снова посмотрим на график функции у = 1/х:

Видно, график не пересекает ось Оу, ведь число х = 0 не входит в область определения функции. Однако можно заметить, что при приближении х к нулю функция неограниченно возрастает:

Получается, что предел функции в точке х = 0 зависит от того, с какой стороны мы приближаемся к этой точке, слева или справа. В связи с этим в математике существует понятие односторонних пределов. Для обозначения пределов, получаемых при приближении к нулю справа, то есть со стороны бОльших чисел, перед ним ставят знак плюс, а при указании предела слева, то есть со стороны мЕньших чисел – знак минус:

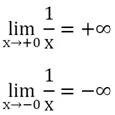
Предел и односторонние пределы – это два разных понятия. Считается, что функция имеет предел в точке только тогда, когда оба односторонних предела в этой точке совпадают.

В качестве ещё одного примера предела функции в точке можно привести зависимость у = tg х, график которой выглядит следующим образом:

В точке х = π/2 функция не определена. Однако видно, что при приближении к этой точке слева функция неограниченно возрастает, а при приближении справа – неограниченно убывает. Это записывается следующим образом:

До этого мы вычисляли пределы функций в точках, где сами функции не определены. Однако пределы можно вычислять и в тех точках, где функция определена. В большинстве случаев (но не всегда) они как раз равны значению функции в этой точке. Например, найдем предел

В точке х = 2 значение функции будет равно 4:

Будут ли односторонние пределы в этой точке также равняться 4? Сначала проверим предел справа

Действительно, получаем значения у, всё более близкие к 4. Аналогично можно убедиться, что и предел слева также равен 4:

Приведем несколько искусственный пример функции, у которой предел в точке не совпадает со значением функции в этой точке. Пусть функция задается с помощью такого графика

Он представляет собой параболу у = х2 с выколотой точкой (2; 4). При этом функция определена в точке х = 2, но имеет там значение, равное единице. Аналитически эту функцию можно описать так:

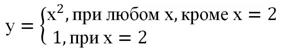
Понятно, что у(2) = 1, однако попытаемся приблизиться к точке х = 2 справа и слева и посмотрим, что получится:

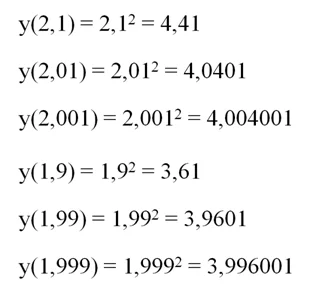
Сразу заметим, что непосредственно в практических задачах пределы почти не используются. В связи с этим эта тема изучается в школьном курсе довольно поверхностно, не дается строгое определение предела функции (предполагается, что это понятие интуитивно понятно), а также не рассматриваются примеры на вычисление пределов функций. С другой стороны, на понятии предела построены почти все строгие рассуждения и доказательства в математическом анализе. В частности, определение понятие производной (которая имеет огромное практическое применение) дается именно с помощью предела. Поэтому полностью исключить пределы из школьного курса нельзя.