Уравнение состояния идеального газа. Газовые законы

Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами

Уравнение состояния идеального газа:

Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.

Уравнение
состояния идеального
газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) —
формула, устанавливающая зависимость
между давлением, молярным
объёмом и абсолютной
температурой идеального
газа.
Уравнение имеет вид:

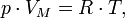
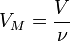
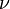
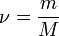
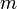
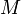
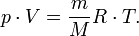
Эта
форма записи носит имя уравнения (закона)
Менделеева — Клапейрона.

В
случае постоянной массы газа уравнение
можно записать в виде:

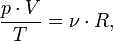
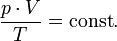
Последнее
уравнение называют объединённым
газовым законом.
Из него получаются законы Бойля —
Мариотта, Шарля и Гей-Люссака:

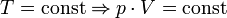
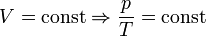
— закон Шарля (второй
закон Гей-Люссака, 1808 г.).А
в форме пропорции

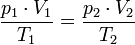
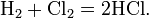
ТЕМА: Решение задач по теме «Уравнение состояния идеального газа»

Учебная: Диагностика степени усвоения знаний по теме «Уравнение состояния идеального газа» и

формирование практических умений по их применению

Развивающая: Развивать интерес к физике, развивать практические умения учащихся при решении

Воспитательная: воспитывать сознательное отношение к учебе и заинтересованность в изучении

Тип урока: урок комплексного применения знаний

I. Организационно мотивационный этап

1) Организация начала урока

2) Проверка домашнего задания

II. Организационно мотивационный этап

3) Актуализация имеющихся знаний.

4) Закрепление знаний и способов действия

6) Первоначальная проверка понимания

III. Рефлексийна заключальны этап

7) Подведение итогов занятия. Выставление оценок

8) Домашнее задание

Приветствие учащихся и учителя. Проверить подготовленность учащихся к уроку, правильную

организацию рабочего места. Отметить отсутствующих в журнале.

Фронтальная проверка выполнения домашнего задания. Обсуждения результатов

II. Операционно познавательный этап.

А) Фронтальный опрос

– Перечислите макроскопические параметры состояния идеального газа ( Р,V,Т)

– Какое уравнение называют уравнением состояния? (Уравнение, выражающее связь между

макроскопическими параметрами состояния вещества)

-В чем заключается основная задача МКТ? ( Установление связи между макроскопическими

параметрами, т.е. нахождение уравнения состояния того или иного тела)

-Сформулировать и доказать закон Дальтона (Давление смеси химически не взаимодействующих

-Записать уравнение Клапейрона. При каких условиях оно справедливо? (PV

– Записать уравнение Менделеева –

Задачи решаются на доске:

1. Определить массу водорода, находящегося в баллоне вместимостью 20 л при давлении 830 кПа,

если температура газа равна 17 °С.

Дано:= 20 л, р = 830 кПа, t = 17 °C, М = 2·103 кг/моль,= 8,31 Дж/(моль·К).

Основное уравнение молекулярно-кинетической теории идеальных газов

Для
вывода основного уравнения
молеку­лярно-кинетической теории
рассмотрим одноатомный идеальный газ.
Предполо­жим, что молекулы газа
движутся хаоти­чески, число взаимных
столкновений меж­ду молекулами газа
пренебрежимо мало по сравнению с числом
ударов о стенки сосуда, а соударения
молекул со стенками сосуда абсолютно
упругие. Выделим на стенке сосуда
некоторую элементарную площадку DS и
вычислим давле­ние, оказываемое на
эту площадку. При каждом соударении
молекула, движущая­ся перпендикулярно
площадке, передает ей
импульс m0v-(-m0v)=2m0v, где т0 —
масса молекулы, v —
ее скорость.

За
время Dt площадки DS достигнут только те
молекулы, которые заключены в объеме
цилиндра с основанием DS и высотой vDt .Число
этих молекул равно nDSvDt (n—концентрация
молекул).

Необходимо,
однако, учитывать, что реально молекулы
движутся к площадке

DS
под разными углами и имеют различ­ные
скорости, причем скорость молекул при
каждом соударении меняется. Для упрощения
расчетов хаотическое движе­ние молекул
заменяют движением вдоль трех взаимно
перпендикулярных направ­лений, так
что в любой момент времени вдоль каждого
из них движется 1/3 моле­кул,
причем половина молекул (1/6)
дви­жется вдоль данного направления
в одну сторону, половина — в противоположную.
Тогда число ударов молекул, движущихся
в заданном направлении, о площадку DS
будет 1/6nDSvDt.
При столкновении с пло­щадкой эти
молекулы передадут ей им­пульс

Тогда
давление газа, оказываемое им на стенку
сосуда,

Если
газ в объеме V содержит N молекул,

характеризующую
всю совокупность моле­кул газа.

Уравнение
(3.1) с учетом (3.2) при­мет вид

Выражение
(3.3) называется основ­ным
уравнением молекулярно-кинетической
теории идеальных газов. Точный
рас­чет с учетом движения молекул по
все-

возможным
направлениям дает ту же формулу.

где Е —
суммарная кинетическая энергия
поступательного движения всех молекул
газа.

Так
как масса газа m =Nm0,
то урав­нение (3.4) можно переписать в
виде

Для
одного моля газа т
= М (М — моляр­ная
масса), поэтому

где Vm —
молярный объем. С другой сто­роны, по
уравнению Клапейрона —
Мен­делеева, pVm=RT. Таким
образом,

Так
как М = m0NA,
где m0—масса
од­ной молекулы, а NА —
постоянная Авогад­ро, то из уравнения
(3.6) следует, что

где k = R/NA—постоянная
Больцмана. Отсюда найдем, что при
комнатной темпе­ратуре молекулы
кислорода имеют сред­нюю квадратичную
скорость 480 м/с, во­дорода — 1900 м/с. При
температуре жид­кого гелия те же
скорости будут соответ­ственно 40 и
160 м/с.

Средняя
кинетическая энергия посту­пательного
движения одной молекулы иде­ального
газа

Давление
газа –
макроскопическое проявление теплового
движения молекул и результат столкновения
молекул со стенками сосуда. При этом
молекулы передают стенкам свой импульс.
Ввиду хаотичности теплового движения
давление газа на все стенки сосуда
одинаково.

Давление
представляет собой среднюю силу,
действующую по нормали на единицу
площади поверхности:

,
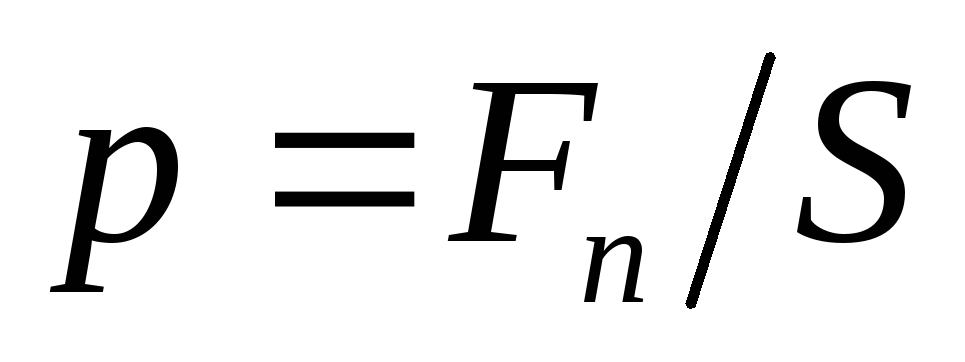
(11)

где
Fn
– проекция вектора силы на нормаль к
поверхности. Сила связана с импульсом
Р
через второй закон Ньютона: P/t
= F.
Давление является скалярной величиной.
Это подтверждает закон Паскаля.

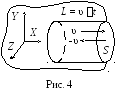
ассмотрим
упрощенный вывод уравнения. Пусть
имеется одноатомный идеальный газ с
концентрацией молекулn.
Выберем на стенке сосуда малую площадку
S
и направим оси координат так, как показано
на рис. 4. Для упрощения расчетов
хаотическое движение молекул заменим
движением вдоль трех осей Х,Y,Z
так, что в любой момент времени вдоль
каждой оси движется 1/3 часть всех молекул,
причем половина из них – в положительном
направлении оси, а другая половина – в
отрицательном. Поэтому можно считать,
что в положительном направлении оси Х
движется только 1/6 часть всех молекул.

За
время t
к площадке S
«подлетят» все молекулы, расположенные
в цилиндре с основанием S
и высотой L
= υ
t.
Число этих молекул равно

При
упругом ударе о стенку молекула массой
m0
изменяет свой импульс на величину (в
проекции на ось Х):

(m0
υ)
= (конеч.) – (нач.) = 
m0
υ

m0
υ
= 
2 m0
υ.

Стенка
сосуда получает равный по величине и
противоположно направленный импульс,
т.е. + 2
m0
υ.

Найдем
суммарный импульс, переданный стенке:

Учитывая
формулу для давления и второй закон
Ньютона, получаем:

Так
как скорости у молекул разные, то следует
пользоваться средним значением квадрата
скорости υ2.
Таким образом, получаем основное
уравнение
молекулярно-кинетической
теории идеального газа:

,
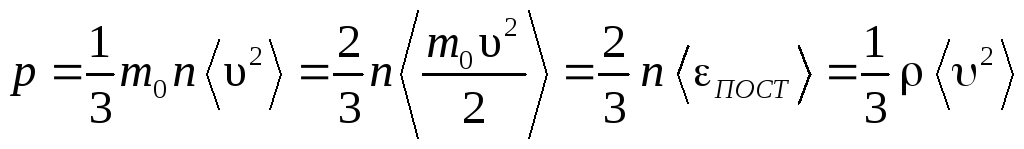
(12)

где
ПОСТ
– средняя энергия поступательного
движения одной молекулы; m0
n
= 
– плотность газа.

Не
следует смешивать понятия «средняя
квадратичная скорость» и «квадрат
средней скорости».

1.
Учитывая, что n
= N/V, уравнение
(12) можно записать в виде

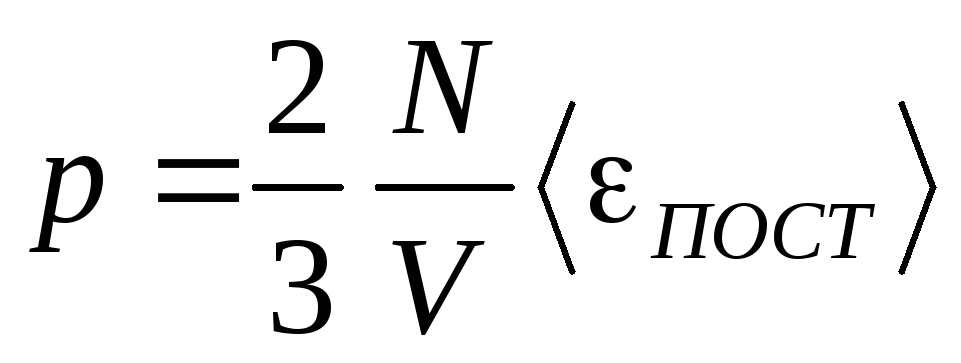
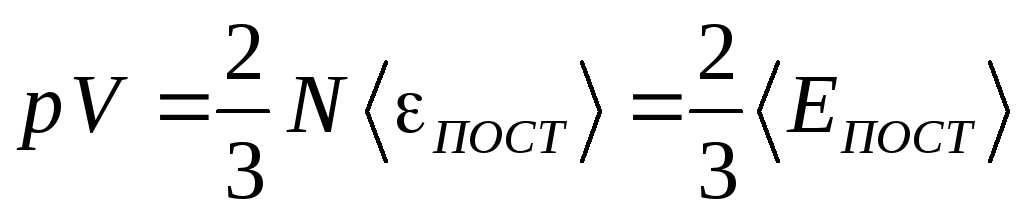
Следовательно,
произведение объёма газа на его давление
равно 2/3 кинетической энергии хаотического
поступательного движения всех молекул
газа, заключенных в этом объёме.

2.
Сравним уравнение (13) с уравнением
Менделеева-Кла­пейрона

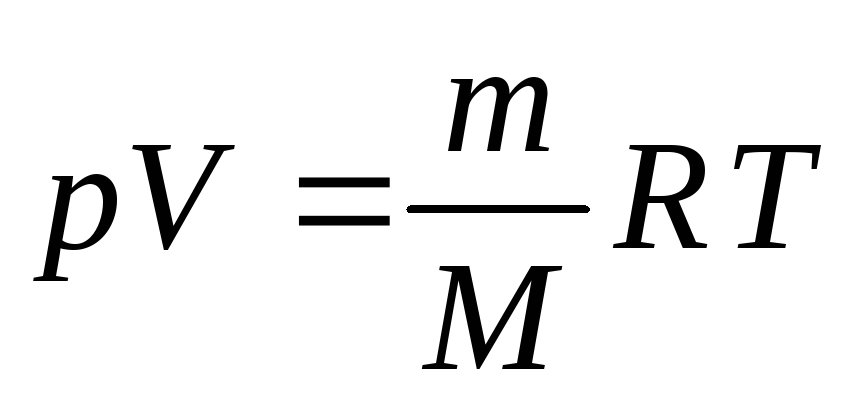
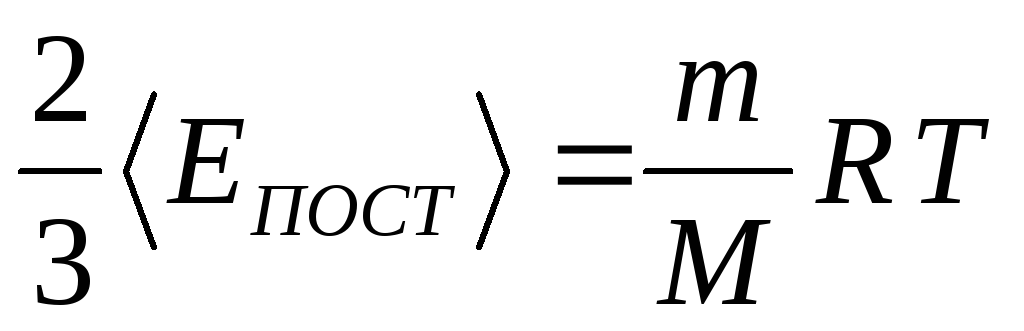
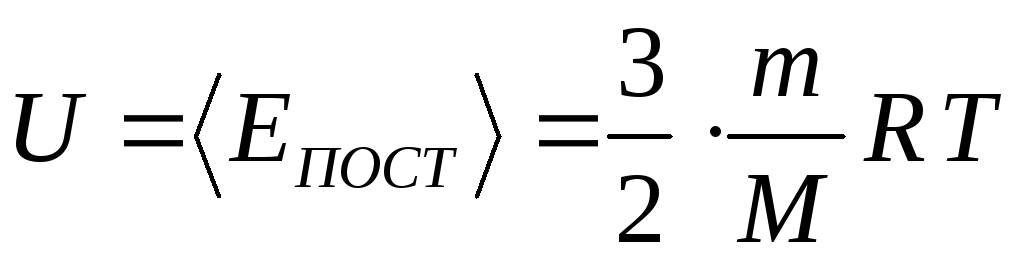
– внутренняя
энергия, определяемая для
одноатомного идеального газа, как
энергия только поступательного движения
молекул.

3.
Подставим в уравнение (12) формулу (5) p
= nkT:

,
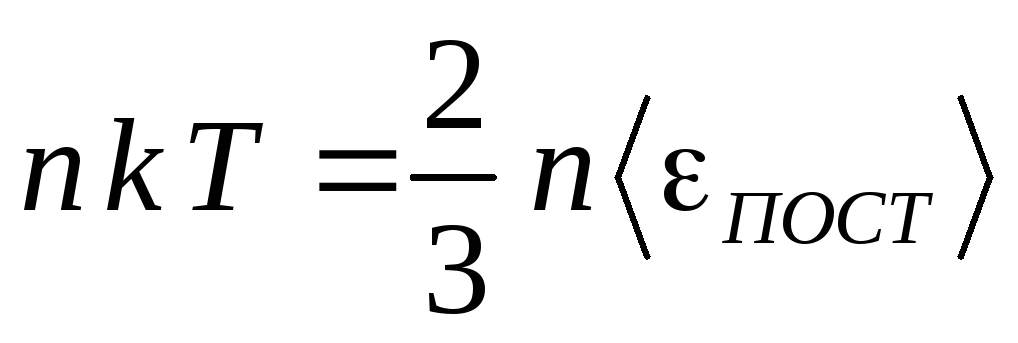
или

.
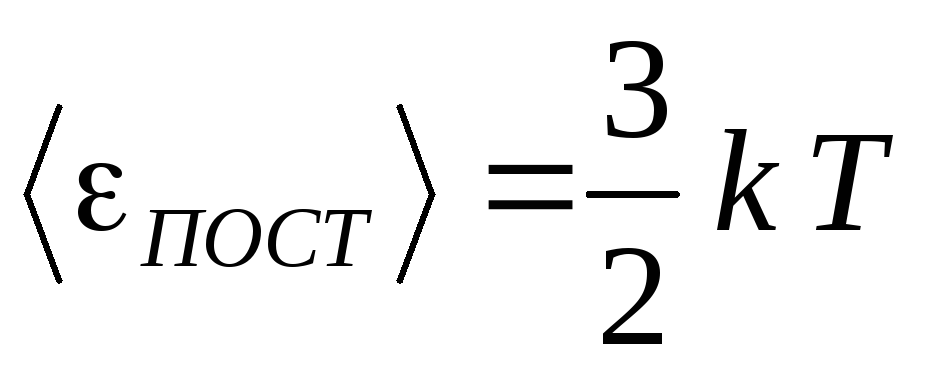
(14)

4.
Из формулы (14) можно найти среднюю
квадратичную скорость:

,
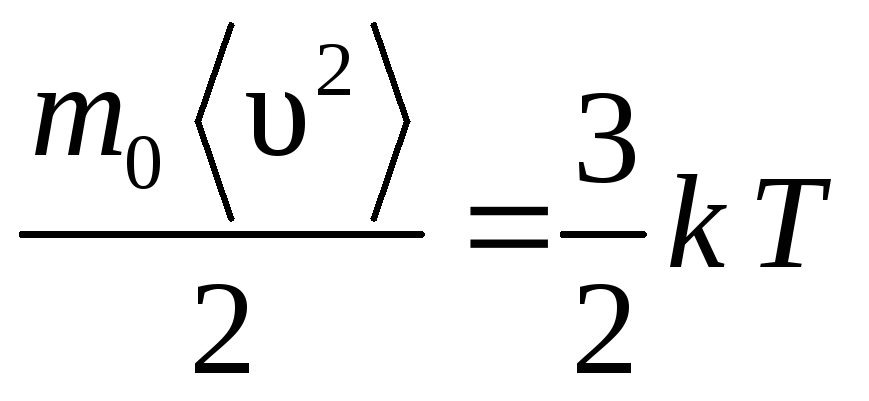
откуда

.
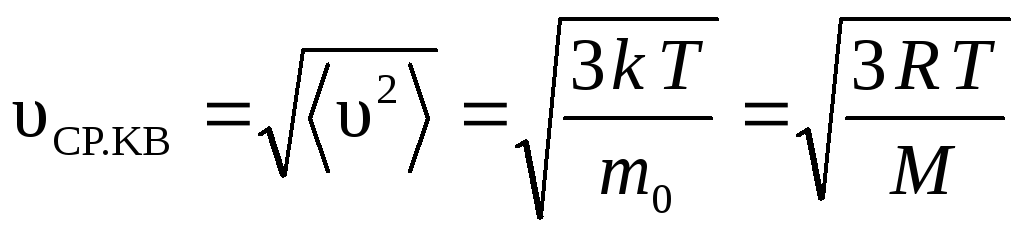
(15)

Числом
степеней свободы
механической системы называется
количество независимых координат, с
помощью которых можно определить
положение системы в пространстве.

Положение
материальной
точки (одноатомный газ)
полностью определяется тремя координатами
(x, y, z)
– 3
степени свободы
(рис. 5).

Положение
абсолютно
твердого тела (трехатомный и многоатомный
газ) может
быть задано тремя координатами центра
масс (x, y, z)
и тремя углами вращательного движения
(, , )
вокруг трех пространственных осей,
проходящих через центр масс (рис. 6) – 6
степеней свободы.

Двухатомная
молекула
(N2,
H2,
O2)
с жесткой связью между атомами имеет 5
степеней свободы
(рис. 7): 3 поступательные (x, y,
z) и 2
вращательные (,
)
вокруг двух осей. Вращение вокруг третьей
оси, проходящей через центры двух атомов,
не меняет положения молекулы в
пространстве.

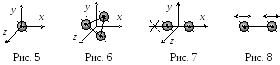
Формула
(12) для давления газа выводилась при
условии, что молекулы являются
материальными точками, имеющими 3
поступательные степени свободы. Поскольку
ни одна из степеней свободы не имеет
преимуществ, то энергия, приходящаяся
на одну степень свободы, равна одной
третьей части от ПОСТ.
Отсюда следует закон
равнораспределения:
на каждую
степень свободы молекулы приходится в
среднем одинаковая кинетическая энергия,
равная
kT/2
.

При
температурах в тысячи градусов
связь атомов в молекуле перестает быть
жесткой, атомы начинают колебаться
(рис. 8). Добавляются
колебательные степени свободы,
которые имеют двойную энергетическую
емкость (энергетический вклад), так как
учитываются и кинетическая, и потенциальная
энергии атомов.

Итак,
средняя энергия одной молекулы равна

,
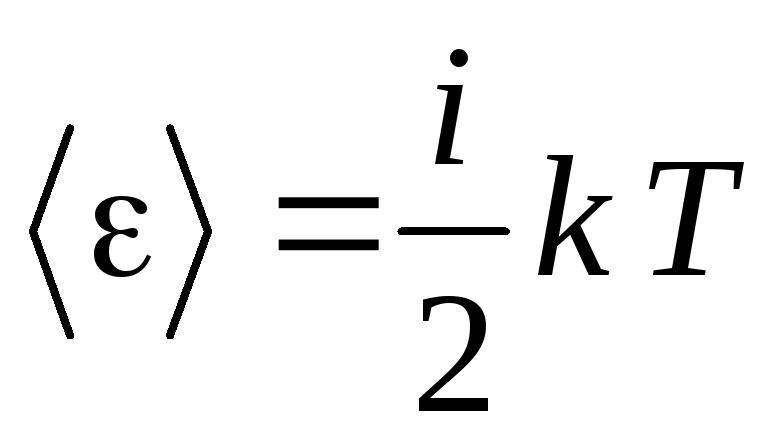
(16)

где
i
– число степеней свободы молекулы,
равное сумме поступательных, вращательных
и колебательных степеней свободы:

.
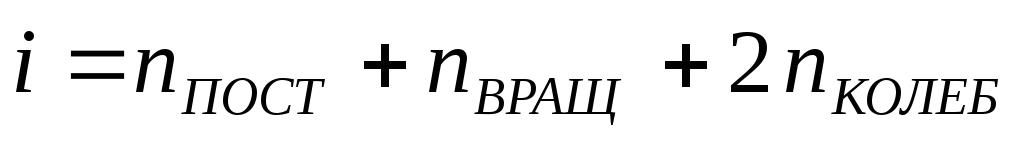
(17)

Формулу
для внутренней энергии идеального газа
можно теперь записать в общем виде:

.
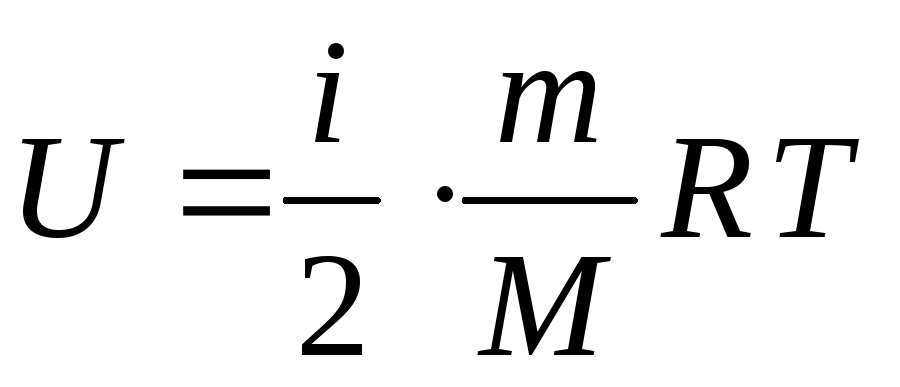
(18)

ТРИЗ-задание
10. Приборы для измерения давления

В
«сильных» изобретениях всегда применяются
физические эффекты. Что такое «физический
эффект»?
В ТРИЗ существует специализированный
указатель
физических эффектов и явлений для
изобретателей.
По материалам сети Интернет изучите
различные конструкции приборов для
измерения давления: манометр,
дифференциальный манометр, вакууммéтр,
барометр, датчики давления. Составьте
список физических эффектов, на основе
которых работают эти приборы.

Соседние файлы в папке папа Жужа

На прошлых уроках мы с вами рассмотрели идеальный газ с
позиций молекулярно-кинетической теории. И выяснили, как зависит давление
идеального газа от концентрации его молекул и температуры.

Однако состояние макроскопической системы считается полностью
определённым, если известны все её макроскопические параметры — давление,
температура и объём. Поэтому нам необходимо установить, как связаны между собой
эти макроскопические параметры.

Уравнение, связывающее температуру, давление и объем
идеального газа в состоянии теплового равновесия, называют уравнением состояния
идеального газа. Несмотря на то, что это уравнение было получено
экспериментально, его легко можно вывести из основного уравнения МКТ:

Как известно, концентрация газа — это число молекул газа в
единице объёма:

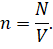
Тогда мы можем записать, что давление газа прямо
пропорционально температуре и числу молекул и обратно пропорционально его
объёму:

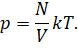
Теперь давайте соберём в левой части уравнения все
макропараметры газа: его давление, объём и температуру:

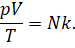
Обратите внимание на правую часть записанного равенства: «Ка»
(k) — это постоянная Больцмана, а N — число молекул газа, которое
при неизменной массе газа тоже является величиной постоянной. Поэтому правая
часть уравнения является константой. Отсюда следует, что при неизменной
массе и неизменном химическом составе газа отношение произведения его давления
и объёма к абсолютной температуре является величиной постоянной:

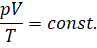
Это и есть уравнение состояния идеального газа.
Впервые оно было получено французским физиком Бенуа Клайпероном в 1834 году,
поэтому его называют уравнением Клайперо́на.

В справедливости уравнения можно убедиться на таком опыте.
Возьмём гофрированный сосуд, объём которого можно менять при помощи винта.
Объём газа измеряется с помощью линейки, а давление — при помощи манометра,
подключённого к сосуду. Температура газа в сосуде равна температуре окружающей
среды и может быть измерена термометром.

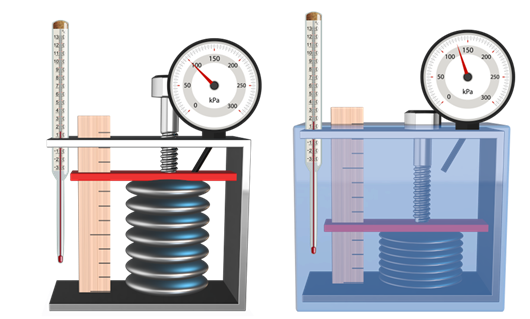
Теперь при помощи винта изменим объём сосуда. А сам сосуд
поместим в горячую воду, тем самым изменив температуру газа и его давление.
Дождёмся теплового равновесия.

Нетрудно заметить, что в пределах погрешности эксперимента отношение
произведения давления и объёма газа к абсолютной температуре действительно
является постоянной величиной:

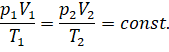
Реальные газы тоже можно описать при помощи уравнения состояния.
Но для этого необходимо выполнение двух условий. Во-первых, давление газа
должно быть таково, чтобы собственный объём всех молекул газа был пренебрежимо
мал по сравнению с вместимостью сосуда, в котором находится газ. А во-вторых,
температура газа должна быть не слишком низкой и не слишком высокой, чтобы абсолютное
значение потенциальной энергии межмолекулярного взаимодействия было пренебрежимо
мало́ по сравнению с кинетической энергией теплового движения молекул.

Получим ещё одно уравнение, связывающее все три
макропараметра. Для этого вернёмся к формуле, в которой мы уже расписали концентрацию
газа через отношение числа его молекул к занимаемому объёму:

Давайте выразим число молекул газа через постоянную
Авога́дро, массу и молярную массу газа из формул для количества вещества:

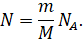
И подставим это значение в исходную формулу: .

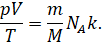
Произведение двух постоянных (Больцмана и числа Авогадро)
называют универсальной (или молярной) газовой постоянной. О её физическом
смысле этой постоянной мы с вами будем говорить немного позднее.

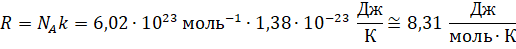
Тогда с учётом введённого обозначения можно записать, что
произведение давления идеального газа и его объёма равно произведению отношения
массы газа к его молярной массе, универсальной газовой постоянной и абсолютной
температуры газа:

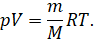
Это уравнение впервые было получено выдающимся русским учёным
Дмитрием Ивановичем Менделеевым в 1874 году. Оно тоже является уравнением
состояния идеального газа, и поэтому его называют уравнением Клайперона —
Менделеева.

Из него вытекают два очень важных следствия. Во-первых, если
выразить из уравнения число молекул газа, то можно заметить, что если различные
газы занимают равные объёмы при одинаковых температурах и давлениях, то число
молекул в них тоже одинаково. Иными словами, из него вытекает установленный
опытным путём закон Авогадро, о котором мы упоминали на прошлых уроках: при
равных давлениях и температурах в одинаковых объёмах любых газов содержится
одинаковое число молекул.

А второе следствие мы рассмотрим на таком примере. Пусть у
нас есть смесь химически не реагирующих разрежённых газов, находящихся в сосуде
вместимостью V. Тепловое движение частиц каждого газа равномерно
распределяет их по всему объёму сосуда. В результате столкновений частиц друг с
другом в смеси устанавливается тепловое равновесие.

Общее число частиц газов в сосуде равно сумме частиц каждого
из газов:

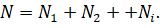
Конечно же, каждый газ в отдельности будет создавать давление
на стенки сосуда. Оно называется парциальным давлением. То есть парциальное
давление — это давление газа, входящего в состав газовой смеси, если бы он один
занимал весь объём, предоставленный смеси, при той же температуре.

Запишем для каждого газа уравнение состояния:

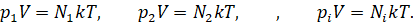
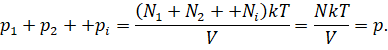
Можно записать, что давление смеси химически не
реагирующих между собой газов равно сумме парциальных давлений каждого из
газов.

Этот закон называют законом Дальтона, так как открыт
он был экспериментальным путём в 1801 году английским учёным Джоном
Дальтоном.

Для закрепления нового материала решим с вами задачу. Баллон
вместимостью 20 л, содержащий газ при давлении 3 МПа и температуре 320 К,
соединили с пустым баллоном вместимостью 5,0 л. Определите давление газа,
которое установилось в баллонах после расширения, если температура газа стала
равной 285 К.

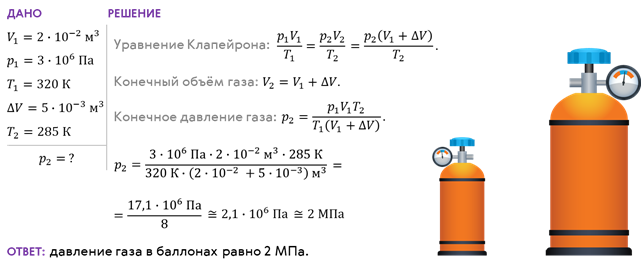
В заключение отметим, что уравнение Клайперона — Менделеева справедливо
для любой массы газа и связывает между собой параметры одного состояния газа.
Использование этого уравнения позволяет описать различные процессы,
происходящие в идеальном газе.

Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения

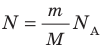
Произведение числа Авогадро

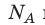
на постоянную Больцмана k называют универсальной газовой постоянной (R): R=

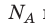
k 8,31 Дж/ (моль⋅К). Заменив в уравнении (*)

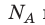
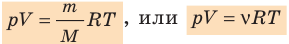
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.

Уравнение Клапейрона

С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (

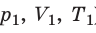
) в состояние (

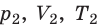
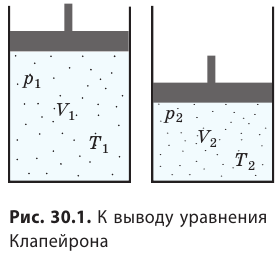
Для каждого состояния запишем уравнение Менделеева — Клапейрона:

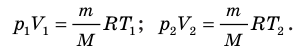
Разделив обе части первого уравнения на

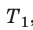
, а второго — на

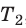
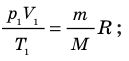
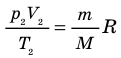
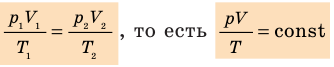
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.

Изопроцессы

Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.

Какой процесс называют изотермическим. Закон Бойля — Мариотта

Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (

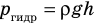
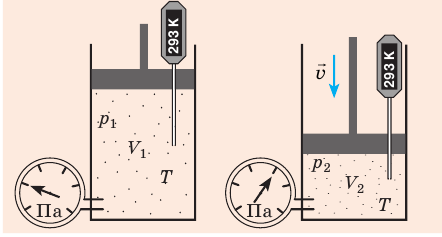
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться

Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.

Пусть некий газ переходит из состояния (

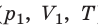
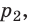
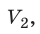
T), то есть температура газа остается неизменной (рис. 30.2). Тогда согласно уравнению Клапейрона имеет место равенство p

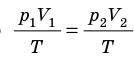
. После сокращения на T получим:

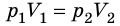
Закон Бойля — Мариотта:

Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:

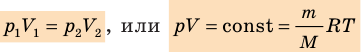
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему:

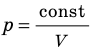
Какой процесс называют изобарным. Закон Гей-Люссака

Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.

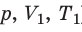
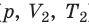
), то есть давление газа остается неизменным (рис. 30.4). Тогда имеет место равенство

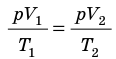
. После сокращения на p получим:

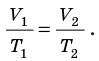
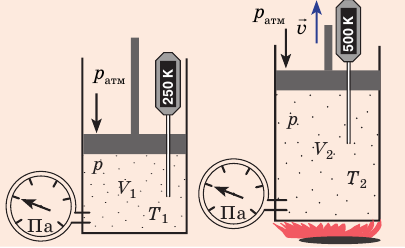
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p

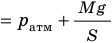
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:

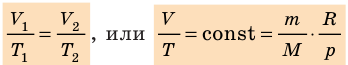
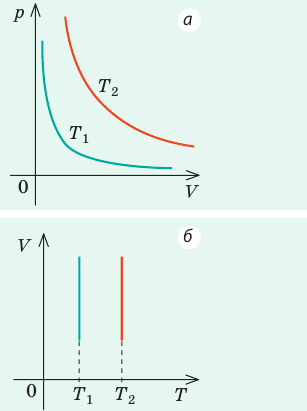
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).

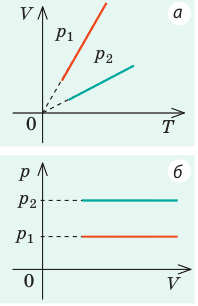
Изохорный процесс. Закон Шарля

Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.

Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.

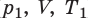
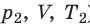
), то есть объем газа не изменяется (рис. 30.6). В этом случае имеет место равенство

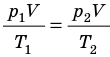
. После сокращения на V получим:

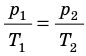
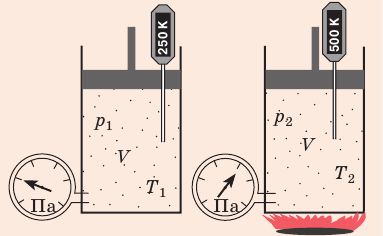
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:

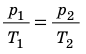
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:

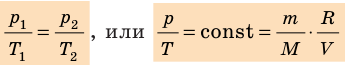
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).

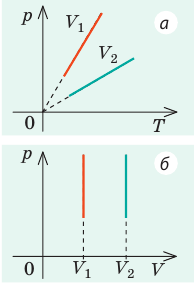
Пример №1

В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?

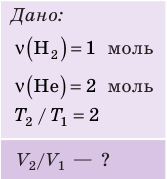
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:

, но использовать закон Бойля — Мариотта нельзя, так как вследствие диссоциации (распада) молярная масса и число молей водорода увеличились в 2 раза:

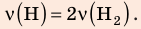
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада:

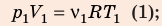
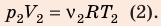
Разделив уравнение (2) на уравнение (1) и учитывая, что

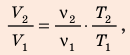
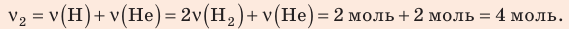
Найдем значение искомой величины:

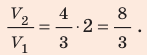
Ответ: примерно в 2,7 раза.

Пример №2

На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.

1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).

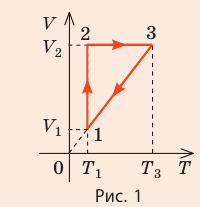
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .

2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)

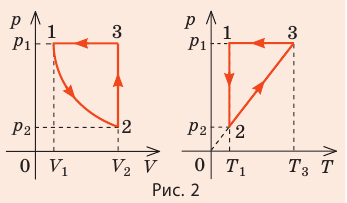
• Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
• Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона): — универсальная газовая постоянная.
• Уравнение Клапейрона:
• Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:

• Температура в физике
• Парообразование и конденсация
• Тепловое равновесие в физике
• Изопроцессы в физике
• Абсолютно упругие и неупругие столкновения тел
• Механизмы, работающие на основе правила моментов
• Идеальный газ в физике
• Уравнение МКТ идеального газа

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Уравнение Менделеева-Клапейрона

Уравнение Клапейрона хорошо описывает изменение в газовых процессах макроскопических параметров некоторого количества газа. Однако, заранее сказать, какими будут эти параметры для конкретной массы некоторого конкретного газа, нельзя. Константа, присутствующая в уравнении Клапейрона должна вычисляться каждый раз заново.

В 1874 г Д. Менделеев сделал вывод, что эта константа прямо пропорциональная количеству вещества газа, то есть отношению общей массы газа $m$ к его молярной массе $М$:

Рис. 2. Д. Менделеев.

Значение температуры чаще всего переносят в правую часть формулы. Окончательно имеем:

Уравнение состояния идеального газа в таком виде называется уравнением Менделеева-Клапейрона. Данное уравнение связывает макроскопические параметры газа с его физическими параметрами.

Постоянная R, присутствующая в уравнении, называется универсальной газовой постоянной. Она равна произведению числа Авогадро на постоянную Больцмана, и представляет количество тепла, которое необходимо сообщить одному молю газа для увеличения его температуры на один кельвин.

Идеальный газ – это теоретическая модель газа, хорошо описывающая поведение реальных газов при невысоких давлениях и температурах. Для описания его макроскопических параметров (температуры, давления и объема) используется специальное соотношение, называемое уравнением состояния. Рассмотрим его подробнее.

«Уравнение состояния идеального газа. Газовые законы»

Установить зависимость между параметрами, определяющими состояние газа.

Сформулировать законы для изопроцессов в газе.

• продолжить формирование понятия макросистемы;
• продолжить формирование умения объяснять законы с молекулярной точки зрения;
• изображать графики изопроцессов.

• развитие познавательного интереса;
• развитие интеллектуальных способностей учащихся;
• развитие предметных и общенаучных умений и навыков;
• развитие навыков самообразования.

• формирование коммуникативных качеств, культуры общения;
• воспитание ответственности у учащихся не только за свои знания, умения, но и за знания каждого обучаемого.

План лекции; (на доске)

• вывод уравнения Менделеева – Клапейрона;
• газовые законы: изотермический
• изобарный;
• изохорный.

I. Организация учебной деятельности учащихся на уроке.

Сообщение темы, цели, задач урока. Стимулирование мотивации учебной деятельности при обучении.

II. Проверка знаний и умений.

Организация самостоятельной работы.

III. Изучение нового материала.

Учитель: (вопросы для повторения)

1. Основное уравнение МКТ имеет вид:

2. Температура — мера средней кинетической энергии. Почему?

, измеряется в Дж, давно известно, что температура измеряется в

3. Как связана абсолютная шкала и шкала Цельсия?

Задача урока: охарактеризовать состояние идеального газа через макропараметры (p, V, T)

Запишем зависимость давления газа от концентрации молекул и температуры

-уравнение состояния идеального газа или уравнение Менделеева-Клапейрона.

Из данного уравнения вытекает связь между давлением, объемом и температурой идеального газа, который может находиться в двух любых состояниях.

Рассмотрим систему , находящуюся в двух состояниях, с параметрами p, V, T.

Запишем уравнения для двух состояний.

(Учащиеся самостоятельно делают вывод и формулируют определение).

Определение: при фиксированной массе отношение произведения давления и объема на температуру есть величина постоянная.

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из трех параметров – давление, объем или температура – остаются неизменными.

Определение: количественные зависимости между двумя параметрами газа при фиксированном значении третьего параметра называют газовыми законами (изопроцессамия).

Рассмотрим каждый из процессов

сформулируем определение. (учащиеся формулируют самостоятельно)

определение: для газа данной массы произведение давления на объем постоянна, если температура газа не меняется.- закон Бойля – Мариотта.

Вывод: (учащиеся самостоятельно по первому рисунку)

изотерма соответствующая более высокой температуре

, лежит на графике выше изотермы, соответствующей более низкой температуре

. Построим графики в координатах PT, VT.

Определение: для газа данной массы отношение объема к температуре постоянно, если давление не изменяется.

Вывод: (самостоятельно по рисунку 2)

изобара соответствующая более высокому давлению

лежит на графике ниже изобары соответствующей более низкому давлению

. Построим графики в координатах PT, PV,Vt.

Определение: при данной массе газа отношение давление газа к температуре постоянно, если объем газа не изменяется.- закон Шарля (1787г.)

Вывод: изохора соответствующая большему объему

лежит ниже изохоры, соответствующей меньшему объему

. Построим графики в координатах PV, VT, Pt.

IV. Повторение опорного конспекта.

V. Закрепление знаний.

VI. Домашнее задание

§70,71 упр.13(1-7), конспект

• Мякишев Г.Я. Физика: учеб. Для 11 кл. общеобразоват. учреждений / Г.Я. Мякишев, Б.Б.Буховцев. – 12-е изд. – М.: Просвещение, 2005.
• Сборники задач.
• CD – диск: Образовательная коллекция. Полный интерактивный курс физики. Физикон. “Открытая физика 1. 1” под. Ред профессора МФТИ С.М. Козелла.

Физика. 10 класс

Физика, 10 класс

Урок 20. Уравнение состояния идеального газа. Газовые законы

Перечень вопросов, рассматриваемых на уроке:

1) уравнение состояния идеального газа и уравнение Менделеева — Клапейрона;

2) закон Дальтона, парциальное давление, закон Авогадро;

3) газовые законы и границы их применимости;

4) графики изохорного, изобарного и изотермического процесса;

5) определение по графикам характера процессов и макропараметров идеального газа;

6) применение модели идеального газа для описания поведения реальных газов.

Глоссарий по теме

Уравнение, связывающее три макроскопических параметра давление, объём и температура, называют уравнением состояния идеального газа.

Парциальное давление – давление отдельно взятого компонента газовой смеси, равно давлению, которое он будет оказывать, если занимает весь объем при той же температуре.

Количественные зависимости между двумя параметрами газа при фиксированном значении третьего параметра называют газовыми законами (изопроцессами).

Процесс изменения состояния термодинамической системы макроскопических тел при постоянной температуре называют изотермическим.

Процесс изменения состояния термодинамической системы макроскопических тел при постоянном давлении называют изобарным.

Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика. 10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 209 – 218.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2009.

Открытые электронные ресурсы по теме урока:

Теоретический материал для самостоятельного изучения

Уравнение Клапейрона при m = const: отношение произведения давления и объёма к температуре есть величина постоянная для постоянной массы газа:

Если изменяется какой-либо макроскопический параметр газа постоянной массы, то два других параметра изменятся таким образом, чтобы указанное соотношение осталось постоянным.

Отношение произведения давления и объёма к температуре равно универсальной газовой постоянной для одного моля идеального газа.

Уравнение Менделеева при v = 1 моль

Произведение постоянной Больцмана и постоянной Авогадро называется универсальной газовой постоянной.

— уравнение состояния идеального газа.

Уравнение состояния идеального газа получило название «уравнение Менделеева-Клапейрона».

Давление смеси химически невзаимодействующих газов равно сумме их парциальных давлений: закон Дальтона.

где pi– парциальное давление i-й компоненты смеси.

Парциальное давление – давление отдельно взятого компонента газовой смеси, равное давлению, которое он будет оказывать, если занимает весь объём при той же температуре.

Один моль любого газа при нормальных условиях занимает один и тот же объём равный:

V0=0,0224м 3 /моль=22,4дм 3 /моль.

Это утверждение называется законом Авогадро

Для газа данной массы произведение давления на объём постоянна, если температура газа не меняется — закон Бойля – Мариотта.

Изотерма соответствующая более высокой температуре T1, лежит на графике выше изотермы, соответствующей более низкой температуре T2.

Если значения давления и температуры в различных точках объёма разные, то в этом случае газ находится в неравновесном состоянии.

Равновесное состояние — это состояние, при котором температура и давление во всех точках объёма одинаковы.

Для газа данной массы отношение объема к температуре постоянно, если давление не изменяется — закон Гей-Люссака.

Изобара соответствующая более высокому давлению p2 лежит на графике ниже изобары соответствующей более низкому давлению p1.

При данной массе газа отношение давление газа к температуре постоянно, если объем газа не изменяется — закон Шарля.

Изохора соответствующая большему объему V2 лежит ниже изохоры, соответствующей меньшему объему V1.

Примеры и разбор решения заданий

1. Установите соответствие между физическими величинами и приборами для их измерения. К каждой позиции первого столбца подберите нужную позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Конспект урока« Уравнение состояния идеального газа»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Тема: Уравнение состояния идеального газа.

— вывести уравнение Менделеева- Клапейрона

— научить решать задачи по этой формуле.

— расширить кругозор учащихся, развитие логического мышления, интеллекта;

— уметь проводить сравнения, делать вводы;

— развить монологическую речь, уметь выступать перед аудиторией.

-научить добывать информацию из дополнительной литературы и из Интернета, анализировать её.

Воспитательные: — прививать интерес к предмету физика;

— научить самостоятельности, ответственности, уверенности;

— создать ситуацию успеха и дружеской поддержки в процессе урока

Оборудование и наглядные пособия:

Компьютер, видеопроектор, экран, презентация «Температура и ее измерение»

1.Тема урока, цель, задачи, содержание.

2. Проверка домашнего задания. Повторение изученного.

а) Презентация учащихся. «Температура и ее измерение»

б)У доски: физический диктант

1.Какая температура по шкале Кельвина соответствует температуре по шкале Цельсия:

2 .Какая температура по шкале Цельсия соответствует температуре по шкале Кельвина по абсолютной шкале:

1. 15К 2. 250К 3. 400К 4.304К

в) Фронтальный опрос

1. Что называется идеальным газом?

2.Назовите условия при которых газ можно считать идеальным.

3.Что называется концентрацией молекул?

4.Почему барабанная перепонка уха не продавливается бомбардирующими ее молекулами воздуха?( Барабанная перепонка уха человека не продавливается бомбардирующими ее молекулами воздуха, так как давления по обе стороны барабанной перепонки примерно равны.)

5.На высоте порядка сотен километров над Землей молекулы атмосферы имеют кинетическую энергию, которой соответствует температура порядка тысяч градусов Цельсия. Почему на такой высоте не плавятся искусственные спутники Земли?

(Спутники не плавятся, потому что на таких высотах концентрация молекул очень мала .)

в) трое учащихся выполняют на компьютерах тест «Молекулярная физика»( диск «Физикон)

3.Объяснение нового материала

Какова масса воздуха в нашем классе?

Ответы записать на доске. Выяснить после решения этой задачи, кто был прав?

1.Три фрагмента из электронного учебника ( Мякишев Г.Я., Буховцев Б.Б., 10 -11 КЛ)

2.Вывод уравнения Менделеева- Клпейрона

Уравнением состояния называется уравнение, связывающее параметры физической системы и однозначно определяющее ее состояние.

В 1834 г. французский физик Б. Клапейрон , работавший длительное время в Петербурге, вывел уравнение состояния идеального газа для постоянной массы газа. В 1874 г. Д. И. Менделеев вывел уравнение для произвольного числа молекул.

В МКТ и термодинамике идеального газа макроскопическими параметрами являются: p, V, T, m.

Мы знаем, что

Произведение постоянных величин есть величина постоянная, следовательно:

4. Решение задач.

Решить следующие задачи:

1.Какова масса воздуха в нашем классе?

Дано: воздух Решение

h =3м V = ав h = 162м 3 закон Менделеева — Клайперона

М=0,029 кг /моль Выразим массу

t =22° C Т= t + 273 =295К

Р=10 5 ПА m =10 5 ·162· 0,029 кг/8,31·295=191,6 кг

Ответ: 191,6 кг

Выяснить, кто был прав.

2. Определите давление 8кг кислорода О 2 , заключенного в

сосуд емкостью V =2м 3 при температуре 47 °С.

3. Определите объем т = 2кг азота при t = 7°С Си давлении

4. Определите массу кислорода О 2 ,заключённого в баллон,

емкостью V = 3 м 3 при температуре t =27°С и давлении

5. Самостоятельная работа

1.Определите объем 4 кг кислорода О 2 , при температуре 17°С и давлении 2,9 ·10 5 Па (молярная масса кислорода равна 32·10· -3 кг/моль)

2. Найти массу углекислого газа при температуре Т=288к и давлении Р=9· 10 5 Па

6.Подведение итогов урока. Домашнее задание.

Анализ и оценка деятельности учащихся на уроке. Учащиеся обсуждают вместе с учителем результативность урока, оценивают свою деятельность

. 1.Сколько правильных ответов вы получили?

1 Объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака

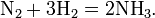
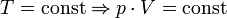
С
одной стороны, в сильно сжатых газах
размеры самих молекул являются сравнимыми
с расстояниями между молекулами. Таким
образом, свободное пространство, в
котором движутся молекулы, меньше, чем
полный объём газа. Это обстоятельство
увеличивает число ударов молекул в
стенку, так как благодаря ему сокращается
расстояние, которое должна пролететь
молекула, чтобы достигнуть стенки. С
другой стороны, в сильно сжатом и,
следовательно, более плотном газе
молекулы заметно притягиваются к другим
молекулам гораздо большую часть времени,
чем молекулы в разреженном газе. Это,
наоборот, уменьшает число ударов молекул
в стенку, так как при наличии притяжения
к другим молекулам молекулы газа движутся
по направлению к стенке с меньшей
скоростью, чем при отсутствии притяжения.
При не слишком больших давлениях более
существенным является второе обстоятельство
и произведение

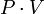
немного
уменьшается. При очень высоких давлениях
большую роль играет первое обстоятельство
и произведение

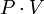
Уравнение состояния для смеси газов

Уравнение состояния идеального газа описывает макроскопические параметры конкретного газа. Однако, в задачах нередко необходимо определять параметры смеси газов с разными молярными массами.

В этом случае применяется закон Дальтона.

Рис. 3. Закон Дальтона.

Давление для каждой из компонент газа вычисляется отдельно, как если бы эта компонента была бы одна. Такое давление называется парциальным, а потом, общее давление смеси, в соответствии с законом Дальтона находится, как сумма парциальных давлений всех компонент.

Основное уравнение состояния идеального газа выводится на основе положений молекулярно-кинетической теории. Согласно этой теории, идеальный газ – это вещество в газообразном состоянии, для которого справедливы следующие допущения:

• молекулы представляют собой материальные точки;
• силы взаимного притяжения молекул отсутствуют;
• молекулы движутся хаотично, при этом каждая движется в соответствии с законами механики Ньютона;
• взаимодействия между молекулами состоят только в абсолютно упругих соударениях.

Согласно основному уравнению молекулярно-кинетической теории, если концентрация молекул газа (количество в единице объема) равно $n$, масса одной молекулы $m_0$, а ее среднеквадратичная скорость $overline $, то давление такого газа равно:

Поскольку молекулы газа считаются материальными точками, то средняя кинетическая энергия движущейся молекулы равна:

Выразим из этого соотношения массу молекулы, и подставим в предыдущее. Получим:

Подставив эту среднюю энергию в предыдущее выражение, получим:

Наконец, выразим концентрацию молекул как отношение их количества к объему ($n=$). В итоге получим:

Данное соотношение было впервые получено и практически доказано в 1834г. Б. Клапейроном, поэтому оно носит название «уравнение Клапейрона».

Что мы узнали?

Уравнение состояния идеального газа связывает объем, давление и температуру (макроскопические газовые параметры) с общей и молярной массой газа. Данное уравнение называется уравнением Менделеева-Клапейрона. Для расчета параметров смеси газов используется закон Дальтона.

Вывод уравнения Менделеева-Клапейрона

Давление идеального газа зависит от концентрации частиц и температуры тела:

Возьмем основное уравнение МКТ, выведенное через кинетическую энергию:

Подставим nkT вместо давления и выразим кинетическую энергию:

Концентрация частиц газа n равна:

Подставим эти величины в уравнение давления идеального газа (p=nkT):

Учитывая, что количество вещества ν также можно определить, если известны масса вещества m и его молярная масса M:

можно привести уравнение к следующему виду:

Закон Бойля-Мариотта — изотермический процесс

Проходит при постоянной температуре: T= const.

P·V = const, то есть для конкретного вещества произведение давления на объем остается постоянным:

Закон Гей-Люссака — изобарный процесс

Проходит при постоянном давлении: P = const.

V/T = const, то есть для конкретного вещества отношение объема и температуры остается постоянным:

Закон Шарля — изобарный процесс

Проходит при постоянном объеме: V = const.

P/T = const, то есть для конкретного вещества отношение давления и температуры остается постоянным:

Понравилась статья, расскажите о ней друзьям:

Уравнение состояния идеального газа Менделеева-Клапейрона с выводом

Уравнение состояния идеального газа показывает корреляцию его основных макропараметров, а именно: объема V, давления P, а также температуры T.

Данную формулу также называют уравнением Менделеева-Клапейрона для идеального газа в честь двух ученых впервые получившего (Бенуа Клапейрон (1799 – 1864)) и применившего (Дмитрий Иванович Менделеев (1834 – 1907)) его.