Урок по математике «Длина окружности и площадь круга» 6кл.план-конспект урока по математике (6 класс)

1. Главная
2. Справочники
3. Справочник по математике 5-9 класс
4. Геометрия
5. Окружность, круг, шар

Окружность – это замкнутая кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки. Заданная точка является центром окружности. На Рис.1 точка О – центр окружности.

Основные характеристики окружности

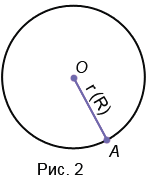
1. Радиус – это отрезок, соединяющий центр с какой-либо точкой окружности. У любой окружности можно провести бесконечно много радиусов, которые будут иметь одну и ту же длину. Обозначают радиус r или R. На Рис.2 представлена окружность с центром в точке О радиусом ОА.

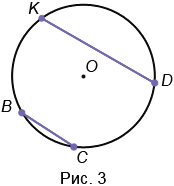
2. Хорда – это отрезок, соединяющий две точки окружности. У любой окружности можно провести бесконечно много хорд. На Рис.3 ВС и KD – хорды окружности с центром в точке О.

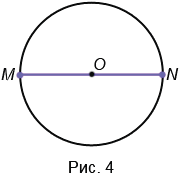
3. Диаметр – это отрезок, соединяющий две точки окружности и проходящий через ее центр (т.е. диаметр – это частный случай хорды). У любой окружности можно провести бесконечно много диаметров, которые будут иметь одну и ту же длину. На Рис.4 МN – диаметр окружности с центром в точке О. Обозначают диаметр d или D. Диаметр в два раза больше радиуса, т.е. d = 2r (D = 2R), откуда r = d : 2 (R = D : 2), следовательно, центр окружности (точка О) является серединой диаметра.

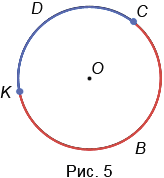
4. Дуга – это часть окружности, ограниченная двумя точками. На Рис.5 KDC и KBC – дуги, ограниченные точками К и С.

Учитель: Чайкова Е. В.

Тема: Длина окружности и площадь круга

Место урока: пятый урок главы «Наглядная геометрия»

Тип урока: изучение нового материала

Формы учебной деятельности: фронтальная, индивидуальная, парная

Методы и приемы обучения: проблемный, частично-новый, практический, взаимоконтроль, самоконтроль, самооценка.

Цель урока: создать условия для вывода формул длины окружности и площади круга.

-изучать формулы длины окружности и площади круга;

-показать применение этих формул при решении задач;

-познакомить учащихся с постоянной величиной π;

-развивать познавательный интерес учащихся в процессе ознакомления с историческим материалом;

-развивать навыки устного счета;

-формировать умение четко и ясно излагать свои мысли;

-воспитывать уважение к математике.

Ребята, вы догадались, о каких геометрических фигурах будет идти речь на уроке?

1. Актуализация опорных знаний.

авайте вспомним, что мы о них знаем. (См. рис. на доске)

азовите центр окружности.

азовите радиус окружности.

Назовите диаметр окружности.

Во сколько раз диаметр длиннее радиуса?

Запишите это формулой на доске.

Есть ли у окружности 2 радиуса различной длины?

А 2 диаметра различной длины?

Ну а поможет нам достичь этой цели ваше домашнее задание.

Что надо было выполнить дома? (измерить длину и диаметр различных окружностей и найти их отношение)

Какие приближенные значения вы получили?

Сравните эти значения с «3» и «4».

Мы можем сказать, что все эти числа приблизительно равны?

Поднимите руки те, у кого так получилось.

1. Изучение нового материала.

Действительно, для всех окружностей отношение длины окружности к длине ее диаметра является одним и тем же числом. Его обозначают греческой буквой «π».

Историческая справка. (сообщение о значениях и возникновении числа π).

Итак, вы внимательно слушали. Скажите, какое приближенное значение имеет число π?

Это все приближенные значения. На самом деле число π не может быть выражено точной дробью.

Обозначим С – длина окружности:

Как из этой формулы найти С?

Число π нам поможет вычислить и площадь круга:

Главное условие – тишина и внимание. Если вы со мной согласны, то поднимите руки вверх и опустите их вниз. Если не согласны, то выполните повороты корпуса вправо и влево. Начнем!

1.По формуле C=2πR можно вычислить длину окружности. (да)

2.Диаметром окружности называется отрезок, соединяющий две точки окружности. (нет)

3.Буквой С обозначают площадь круга. (нет)

4.По формуле S=πR² можно вычислить площадь круга. (да)

5.Часть плоскости, ограниченная окружностью, называется кругом. (да)

6.Число π≈22/7. (да)

7.По формуле С=πd² можно вычислить длину окружности. (нет)

7. Закрепление. Решение задач.

№10.66 (1,3), 10.69 (1,3), 10.67 (1,3), 10.71

П. 10.6 №10.66 (2), 10.67 (2), 10.69 (2)

Найти стихи, которые помогают запомнить формулы длины окружности и площади круга, число π.

1. Рефлексия. Выставление оценок.

Выбрать 1-2 предложения и закончить их (устно).

• Обобщить и систематизировать умения и навыки по теме «Длина окружности.
  Площадь круга».

• Развивать логическое мышление, способствовать расширению кругозора, развитию математической речи.

• Развивать творческое и умственное мышление, побуждать учащихся к самоконтролю, взаимоконтролю, самоанализу, воспитанию эстетических качеств.

Оборудование: мультимедийный проектор и компьютер, презентация «Длина окружности. Площадь круга».

1. Организационный момент.

Приветствие, сообщение темы и цели урока.

2. Актуализация знаний и умений.

1) Назовите: 1) радиус; 2) диаметр окружности (слайд 2).
2) Назовите формулу для вычисления: а) длины окружности; б) площади круга (слайд 3).
2) Вычислите длину окружности: а) радиуса 2 см; б) диаметра 2см (слайд 4 – 5).
3) Вычислите площадь круга: а) радиуса 2 см; б) диаметра 2см (слайд 6 – 7).
4) Как изменится длина окружности, если ее радиус: а) увеличили в 4 раза; б) уменьшили в 4 раза (слайд 8 – 9).
Вывод: Длина окружности прямо – пропорциональна её радиусу.
7) Сравните длины голубой и черной линий (слайд 10).
Ответ: Длина черной и голубой линий одинаковы. (2πR/2=πR – длина синей линии. (2π(r1+r2))/2=πR – длина черной линии).

3. Выполнение учащимися индивидуально письменных заданий с последующей проверкой.

№1 Вычислите длину окружности: а) радиуса 1,54см; б) диаметра 2,12см, π≈3,14.
№2 Вычислите площадь круга, длину окружности: а) радиуса 1,2см; б) диаметра 2,2см, π≈3,14.
№3 Вычислите площадь круга, если длина окружности 12,56см, π≈3,14.
№4 Вычислите диаметр окружности, если ее длина равна: а) 56,52дм; б) 37,68см; π≈3,14.
№5 Вычислите площадь круга, если диаметр 6см, π≈3,14.

4. Задания по готовым рисункам.

Устно:
(Обсуждение с детьми хода решения задач; на слайдах показан ход решения.)

№1 Найдите площадь кольца, если радиусы 3см и 4 см, π≈3 (слайд 11 – 12).
1)42*3=48(см²) – площадь большого круга.
2)32*3=27(см²) – площадь маленького круга.
3)48-27=21(см²) – площадь кольца.

№2 Из круга r=4см вырезали квадрата, со стороной 2см. Найдите площадь закрашенной фигуры π≈3 (слайд 13 – 14).
1)42*3=48(см²) – площадь круга.
2)22 =4(см²) – площадь квадрата.
3)48-4=44(см²) – площадь закрашенной фигуры.

№3 Из квадрата со стороной 6см вырезали круг, наибольшей площади. Найдите площадь закрашенной фигуры, π≈3 (слайд 15 – 16).
1)62 =36(см²) площадь квадрата.
2)6/2=3(см) – длина радиуса.
2)32*3=27(см²) – площадь круга
3)36-27=9(см²) – площадь закрашенной фигуры.

№4 Сторона квадрата 6см. Найдите площадь закрашенной фигуры (слайд 17 – 18).
1)62 =36(см²) площадь квадрата.
2)6/2=3(см) – длина радиуса.
2)32*3=27(см²) – площадь круга.
3)27/2=13,5(см²) – площадь полукруга.
3)36-13,5=22,5(см²) – площадь закрашенной фигуры.

№5 Найдите площадь закрашенной фигуры, если сторона квадрата равна 4 см, π≈3 (слайд 19 – 23).
1)42 =16(см²) площадь квадрата.
2)4/2=2(см) – длина радиуса.
2)22*3=12(см²) – площадь круга. (Кругов получается два)
3)12*2=24(см²) – площадь всех полукругов.
3)16+24=40(см²) – площадь закрашенной фигуры.

№6 На сторонах квадрата, как на диаметрах, построили полукруги внутри квадрата. Найдите площадь закрашенной фигуры. Сторона  квадрата 4 см, π≈3 (слайд 24 – 26).
1)4/2=2(см) – длина радиуса.
2)22*3=12(см²) – площадь круга. (Кругов получается два)
3)12*2=24(см²) – площадь всех полукругов.
4)42 =16(см²) площадь квадрата.
5)24-16=8(см²) – площадь закрашенной фигуры.

№1 Диаметр колеса телеги равен 80 см, колесо сделало 500 оборотов, π≈3,14. Найдите путь лошади? (слайд 27).

№2 Найдите длину окружности и площадь круглого стола, диаметр которого равен 100 см, π≈3,14. (слайд 28).

№3 Какую толщину имеет дерево на высоте 0,5м, если длина тесьмы, которой опоясано дерево на этой высоте, равна 157см? π≈3,14. (слайд 29).

5. Подведение итогов (характеристика работы учащихся, определение типичных ошибок и пробелов в знаниях и умениях, а также путей их устранения и совершенствования).

6.Постановка задания на дом.

–
Паша, чем ты занимаешься? – спросил у друга Саша.

–
Решил обновить шины на моём велосипеде, – ответил Паша. – Чтобы купить новые,
мне нужно знать размер колеса.

–
И как же ты узнаешь этот размер? – решил уточнить Саша.

–
Для этого мне нужно измерить длину шины велосипедного колеса, – ответил Паша.

–
А как измерить эту длину? – удивился Саша. – Ты же не будешь для этого резать
шину?

–
Да это же совсем просто! – улыбнулся Паша. – Я взял сантиметровую ленту у мамы
и ей измерил длину шины.

–
И точно, всё просто! – согласился Саша. – И что же у тебя вышло?

–
Длина шины моего колеса равна 189 сантиметрам.

–
Это значит, размер твоего велосипедного колеса 189 сантиметров? – решил
уточнить Саша.

–
Нет, – ответил Паша, – а вот чтобы выяснить размер велосипедного колеса, нужно
как-то из длины шины выразить диаметр. А как это сделать, я не знаю.

–
Ну чего же ты расстраиваешься?! – воскликнул Саша. – Давай спросим у Мудряша.
Он точно сможет нам помочь.

–
Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и
выполним устные задания, – предложил Мудряш.

–
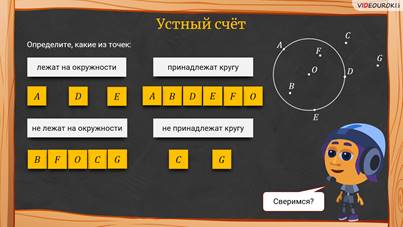
Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было
получиться!

–
Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Всё правильно. Чтобы
выяснить, какой размер у велосипедного колеса, нужно знать его диаметр. Но для
начала давайте определим, какую форму имеет велосипедное колесо.

–
Велосипедное колесо имеет форму окружности, – ответили мальчишки.

–
Верно! – согласился Мудряш. – Зная длину окружности, можно вычислить её
диаметр.

–
А как измерить длину окружности? – решили спросить мальчишки. – Ведь длину окружности
не измеряешь сантиметровой лентой. Да и разрезать её не получится, чтобы
измерить линейкой.

–
Изобретательный ум человека придумал много способов решения этой задачи, –
начал Мудряш. – Обозначим длину окружности буквой l.
Несложно догадаться, что длина l
окружности зависит от длины её диаметра d,
а именно: чем больше диаметр, тем больше будет длина окружности. Другими
словами, длина окружности прямо пропорциональна её диаметру.

Но,
оказывается, для всех окружностей отношение длины окружности к её диаметру
является одним и тем же числом .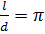

Это
число обозначают греческой буквой. Читают эту букву .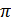
Это начальная буква греческого слова perimetron, которое и означает
«окружность». Запомните! Отношение длины окружности к её диаметру
равно числу .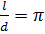
Отсюда можем записать, что длину окружности можно вычислить по формуле .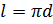
Вы уже знаете, что диаметр в 2 раза больше радиуса, следовательно, можно
получить ещё одну формулу для вычисления длины окружности: .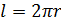

–
Тогда получается, чтобы выразить диаметр окружности, а в моём случае — диаметр
велосипедного колеса, – начал Паша, – нужно длину окружности разделить на это
число ?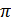

–
Правильно! – ответил Мудряш.

–
Но разве можно разделить число на букву? – спросил Паша. – Или это загадочное
число 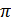 имеет
какое-то значение?

–
Давайте немного коснёмся истории, – предложил Мудряш. – Ещё в Древнем Египте
было замечено, что длина окружности примерно в 3 раза больше её диаметра, то
есть древние египтяне считали, что число .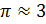
Затем древние учёные установили, что число .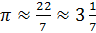
Позднее выяснилось, что  –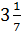
это достаточно точное, но всё-таки приблизительное значение числа .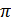
Со временем великий древнегреческий учёный Архимед доказал, что число .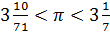
Французский математик Франсуа Виет вычислил значение числа 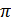 с
девятью правильными знаками после запятой ().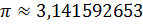
А вот уже в 18 веке математики установили, что число 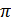 относится
к таким числам, точное значение которых записать невозможно ни с помощью
обыкновенных, ни с помощью десятичных дробей, то есть число 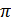 нельзя
представить в виде конечной десятичной дроби или бесконечной периодической
десятичной дроби. Оно выражается бесконечной непериодической десятичной дробью.
Учёные до сих пор проявляют большой интерес к числу .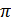
С появлением современных компьютеров можно вычислить число 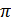 с
огромной точностью. Так, например, в 1987 году благодаря расчётам на компьютере
братья Чудновские вывели число 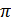 с
миллионом символов после запятой. В 2009 году учёные из Японии рассчитали на
суперкомпьютере значение числа 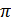 с
двумя с половиной миллионами знаков после запятой. В этом же году программист
из Франции Фабрис Беллар с помощью компьютера получил 2 699 999 990 000
символов после запятой. Только представьте себе, его расчёты длились 131 день.

–
Ого! – воскликнули ребята. – Это число 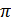 такое
большущее!

–
Не пугайтесь числа ,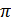
– продолжил Мудряш. – При вычислениях мы чаще всего будем использовать
приближённое значение числа 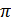 с
точностью до сотых, то есть .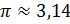

–
Тогда получается, что диаметр моего велосипедного колеса равен 189 разделить на
3,14, – начал считать Паша, – и приближённо равен 60 сантиметрам.

–
Молодец! – похвалил Пашу Мудряш. – Кстати, с помощью нашего интересного числа 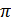 можно
вычислить ещё и площадь круга. Запомните! Площадь круга 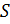 радиуса
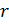 вычисляется
по формуле: .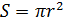
Для вывода этой формулы наших математических знаний пока ещё недостаточно. Как
получают эту формулу, вы узнаете в старших классах. Поэтому пока для решения
задач мы будем использовать готовую формулу.

–
А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько
заданий.

Задание
первое: найдите длину окружности, если известно, что: её
радиус равен 24 сантиметрам; её диаметр равен 9,5 дециметра. Число 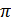 округлите
до сотых.

Решение: мы
знаем, что длина окружности вычисляется по формуле .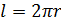
Подставим наши значения в формулу. Посчитаем. Получим, что длина окружности приближённо
равна 150,72 сантиметра.

Перейдём
к следующему условию. Нам известен диаметр окружности. Мы знаем, что длину
окружности можно вычислить по формуле .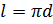
Подставим наши значения. Посчитаем. И получим, что длина окружности приближённо
равна 29,83 дециметра.

Задание
второе: найдите диаметр колеса велосипеда, если известно, что
на расстоянии 450 метров оно сделало 150 оборотов. Число 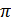 округлите
до сотых. Результат округлите до сотых метра.

Решение: для
начала вычислим, чему равна длина окружности колеса. Так как на расстоянии 450
метров колесо сделало 150 оборотов, то 1 оборот колеса равен 3 метрам. Полный
оборот колеса – это и есть длина окружности. А теперь вычислим диаметр колеса.
Из формулы длины окружности выразим диаметр .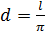
Подставим наши значения. Получим, что диаметр колеса примерно равен 0,955
метра. В условии задачи сказано, что ответ нужно округлить со сотых. Так как
после округляемого разряда стоит цифра 5, то к разряду сотых добавим 1.
Получим, что диаметр колеса приближённо равен 0,96 метра. Запишем ответ.

Задание
третье: вычислите площадь круга, если его диаметр равен 6
сантиметрам. Число 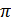 округлите
до сотых.

Решение: мы
знаем, что площадь круга можно вычислить по формуле .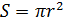
Диаметр круга в 2 раза больше его радиуса. Следовательно, радиус нашего круга
равен 3 сантиметрам. Подставим наши значения в формулу площади круга.
Посчитаем. Получим, что площадь круга приближённо равна 28,26 см².

И
последнее задание: Сторона квадрата равна 8 сантиметрам. Найдите
площадь закрашенной части круга. Число 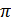 округлите
до целых.

Решение: по
рисунку видно, что сторона квадрата является диаметром круга. Значит, диаметр
круга равен 8 сантиметрам. Мы знаем, что площадь круга можно вычислить по
формуле .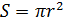
Так как диаметр круга в 2 раза больше его радиуса, то радиус нашего круга равен
4 сантиметрам. Подставим наши значения в формулу площади круга. Посчитаем.
Получим, что площадь всего круга приближённо равна 48 см². По
условию задачи нам нужно выяснить, чему равна площадь закрашенной части круга.
Нетрудно заметить, что эта закрашенная часть составляет половину круга. Значит,
площадь закрашенной части круга приближённо равна 24 см². Не забудем
записать ответ.

Цель урока: формирование и развитие у учащихся личностных; регулятивных; познавательных и коммуникативных способов действия; вывести формулы длины окружности и площадь круга и показать ее применение при решении задач.

• изучить формулы длины окружности и площади круга;
• показать применение этих формул при решении задач;
• познакомить учащихся с постоянной величиной π;
• отработать навыки проведения эксперимента и с помощью экспериментальных данных делать выводы.

• развивать познавательный интерес учащихся в процессе ознакомления с историческим материалом;
• развивать навыки устного счёта;
• развивать творческую и мыслительную деятельность учащихся, их интеллектуальные качества: способность к «видению» проблемы;
• формировать умения чётко и ясно излагать свои мысли;
• развивать пространственное воображение учащихся.

• прививать учащимся навык самостоятельности в работе, учить трудолюбию, аккуратности;
• воспитывать умение работать с имеющейся информацией в необычной ситуации;
• воспитывать уважение к математике, умение видеть математические задачи в окружающем нас мире.

Тип урока: урок изучения нового материала.

Форма работы: индивидуальная, работа в парах, коллективная.

Оборудование: раздаточный материал; для практической работы: нитки, ножницы, циркуль, линейка, карандаш.

1. Практическая работа по теме «Длина окружности и площадь круга». 6 класс

Цель: Проверить знания формул вычисления длины окружности и площади круга.

Пособие: круг с ниткой.

1. Найти длину окружности, практическим путем (с помощью нитки)
2. Измерить линейкой диаметр окружности. Найти длину окружности по формуле.
3. Найти радиус окружности. Найти площадь круга.

1) Длина нитки = длина окружности =

2) d =

C = Пd

3) R =

S = ПR²

1) Длина нитки = длина окружности =

d =

C = Пd

C =

R =

S = ПR²

S =

Историческое сообщение о числе π

Символ π означает отношение длины окружности к ее диаметру. Впервые в этом смысле символ π был использован У.Джонсом в 1707, а Л.Эйлер, приняв это обозначение, ввел его в научный обиход. Еще в древности математикам было известно, что вычисление значения π и площади круга – задачи, тесно связанные между собой. Древние китайцы и древние евреи считали число π равным 3. Значение числа π, равное 3,1605, содержится в древнеегипетском папирусе писца Ахмеса (около 1650 до нашей эры). Около 225 до нашей эры Архимед, используя вписанный и описанный правильные 96-угольники, приближенно вычислил площадь круга с помощью метода, который привел к значению ПИ, заключенному между 31/7 и 310/71. Другое приближенное значение π, эквивалентное обычному десятичному представлению этого числа 3,1416, известно что ван Цейлен (1540-1610) вычислил значение ПИ с 32 десятичными знаками

Вычисление как можно большего числа точных цифр числа с помощью компьютера занимает математиков и в настоящее время. Так, в 1988 году, японский ученый Ясума Канеда вычислил 400 млн точных цифр после запятой. Это не только спортивный интерес, необходимо и для изучения случайных процессов. В школьном же курсе математики π =3,14.

День числа π (пи) отмечается любителями математики 14 марта в 1:59:26.

В это время читают хвалебные речи в честь числа π, его роли в жизни человечества, рисуют антиутопические картины мира без π, пекут и едят «пирог» с изображением греческой буквы «пи» или с первыми цифрами самого числа, пьют напитки и играют в игры, начинающиеся на «пи», решают математические головоломки и загадки, водят хороводы вокруг предметов, связанных с этим числом.

2. Практические задачи

1.Найти радиус колеса, у которого длина окружности 125,6 см.

Решение: R= 125,6:( 2*3,14)=20 см.

2. Найти длину окружности круглой комнаты, если диаметр её D = 5,5 м.

Решение: С=5,5*3,14=17,27 см

1. Организационный момент (1-2 минуты)

Я рада вас всех видеть. Чтобы начать работу, проверим, всё ли готово к уроку.

2. Постановка цели и мотивация (3-5 минут)

Тема нашего урока – Длина окружности и площадь круга. Запишем ее в тетрадь.

Ребята, давайте перед практической работой сделаем разминку. Сядьте ровно.

Покажите мне руками маленькую окружность. А теперь представьте, что наша окружность раздувается, становится все больше и больше. Показываем, вот какая получилась окружность. А теперь поднимаем эту окружность над собой и держим над головой. Представим, что подул ветер и наша окружность наклоняется сначала влево, потом вправо. А теперь представим, что окружность превратилась в воздушный шарик и отпускаем ее.

Молодцы! Приступаем к работе!

Практическая работа №1 (15 минут)

Учащиеся выполняют практические задания по команде учителя и записывают свои наблюдения (учитель может все проделывать на доске, если класс не достаточно подготовлен к самостоятельной работе, или предложить ученикам работать в парах).

1. На картонном листе начертить окружность с произвольным радиусом, отметить её центр, записать значение радиуса в миллиметрах(r) и значение диаметра в миллиметрах (d).
2. Провести клеем-карандашом по окружности и, пока клей не высох, проложить нитку точно по контуру окружности и аккуратно отрезать её на стыке.
3. Снять нитку с картона и очень точно измерить её длину в миллиметрах. Этот размер назовем длиной окружности (C). Записать значение C.
4. Найти отношение C/d с помощью калькулятора, округлить получившуюся дробь до тысячных, до сотых, до десятых, до целых. Сделать соответственные записи.

Индивидуальная работа. Каждый работает самостоятельно, используя указания учителя, делают соответственные записи в тетради.

C = 195 мм, С = 292 мм

d = 60 мм, d = 90 мм

C/d = 195 : 60 = 3,25

C/d = 292 : 90 = 3, 2444)

Далее ученики называют свои результаты и замечают, что, хотя окружности были построены у всех разные, отношения длины к диаметру получились примерно одинаковые отношения больше 3, но меньше 4. Значит, можно записать:

3 < C/d < 4.

Происходит первичное осознание полученных результатов, а именно: отношение длины окружности к ее диаметру есть число постоянное.

Первое знакомство с числом Пи.

Историческая справка (5-7 мин)

Практическая работа №2. Вывод формулы длины окружности. (5-7 минут)

Итак, мы имеем следующее соотношение: C/d = π. Выведем из этой формулы С = πd или С = 2πR. Эта формула называется формулой длины окружности. Чтобы найти длину окружности, надо знать её радиус или диаметр.

Задание. Вычислить по формуле длину своей окружности. Сравнить результаты, полученные опытным путем и с помощью применения формул.

Практическая работа №3. Вывод формулы площади круга. (15 минут)

Учащиеся выполняют практические задания по команде учителя (учитель может проделывать все на доске).

1. На листе цветной бумаги начертить окружность с произвольным радиусом и провести фломастером по её контуру.

2. Разделить круг с помощью линейки и карандаша на несколько секторов, затем разрезать его. (см. рис.1) Заметим, что не следует делить круг на меньшее, чем 8 секторов.

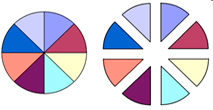
3. В одном из секторов следует провести радиус, делящий его на 2 равных сектора, которые назовём крайними (см. рис.2) и отложить.

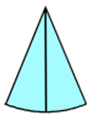
4. На картонном листе провести горизонтальную прямую и приклеить вдоль неё сектора, как показано на рис.3. (На рис.3,а – круг разделен на 8 секторов, на рис.3,б – на 16 секторов). Крайние сектора приклеить по краям. Заметно, что получившаяся фигура при увеличении количества секторов становится очень похожей на прямоугольник. Значит, и её площадь можно найти по формуле площади прямоугольника. Ширина нашего прямоугольника равна радиусу окружности (R), а длина прямоугольника равна половине длины окружности (C/d). Площадь прямоугольника равна произведению длины на ширину, т.е. S = RC/2, а т.к. С=2πR, значит, S = R2πR/2или S = πR².

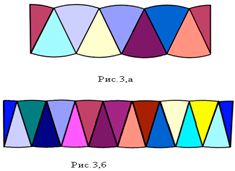
Так как прямоугольник был составлен из частей круга, то их площади равны. Значит, площадь круга равна: S = πR².

Другой способ вывода формулы площади круга вы найдете в учебнике.

Необходимо распределить слова на две группы “Окружность” и “Круг”.

На доске, стенах класса с помощью магнитов и скотча прикреплены слова, ученики одновременно по команде учителя распределяют слова по группам. Время выполнения ограниченно.

(Плоская тарелка, блин, пяльцы для вышивания, резинка для волос, компакт-диск, покрышка для колес, обруч (халахуп), кольцо, бублик, колечко колбасы).

Молодцы! Продолжаем нашу работу!

Подведение итогов. Рефлексия (5-7 минут)

На этом уроке мы рассмотрим одни из самых древнейших геометрических фигур: окружность и круг.

Определим, какими элементами характеризуются круг и окружность, в чем сходство и различие этих фигур.

Узнаем, как рассчитать длину окружности и площадь круга.

Мы часто встречаем такие понятия, как окружность и круг.

Давайте попробуем разобраться, что называют окружностью, а что кругом.

Окружность – это замкнутая плоская кривая, все точки которой удалены на одинаковые расстояния от заданной точки, называемой центром окружности.

Центр окружности– это точка, которая находится на одинаковом расстоянии (равноудаленная) от любой точки окружности, ее обозначают обычно заглавной буквой О.

По сути, окружность – это изогнутая линия. Наглядно представить данную геометрическую фигуру можно, обведя стакан или блюдце карандашом, – оставшийся нарисованный след и будет окружностью.

Круг – это часть плоскости, ограниченная окружностью. Можно также сказать что это часть плоскости, которая находится внутри линии окружности.

Круг – плоская фигура, ее можно получить, закрасив окружность или вырезав его из бумаги по контуру окружности.

Свои имена окружность и круг приобрели не сразу.

В древние времена специальных названий для этих фигур не существовало. Люди пытались описать различные геометрические формы, сравнивая объекты. Например, говоря про что-то круглое, говорили: «такой, как солнце» или «такой, как орех» и т.п.

Только в Древней Греции окружность и круг приобрели себе свои названия.

Круг всегда привлекал к себе внимание как самая простая фигура из кривых, но самая загадочная.

В живой и неживой природе круги и окружности встречаются как на макроуровнях, так и на микроуровнях. Например, движение электронов вокруг атомного ядра; вращение планет вокруг солнца; распространение волн на воде от упавшего груза; образование солнечного и лунного гало; срез дерева; зрачок глаза у человека и многое другое.

Рассмотрим подробней элементы, характерные для окружности.

Радиус окружности– это отрезок, соединяющий центр окружности и любую другую точку, расположенную на линии окружности.

С латинского радиус (radius)- луч, спица колеса. Радиус не сразу приобрел себе такое название.

Слово радиус впервые встречается в 1569 году у французского ученого П. Рамуса, а общепризнанным становится к концу XVII века.

Радиус обозначается маленькой латинской буквой (r) или заглавной (R).

В окружности можно провести столько же радиусов, сколько точек имеет линия окружности; все эти радиусы равны.

Диаметр – это отрезок прямой, проходящий через центр окружности и соединяющий две точки на этой окружности.

Диаметр в переводе с греческого (diametros) – поперечник.

Обычно диаметр обозначают латинской маленькой буквой d или заглавной D.

По величине диаметр равен двум радиусам, лежащим на одной прямой.

d = 2r

Следовательно, радиус- это половина диаметра.

r = d: 2

Радиус окружности равен 6 см.

Чему равен диаметр окружности?

r = 6 см

d = 2r

d = 2r= 2*6 = 12 (см) диаметр окружности

Ответ: d= 12 см

Диаметр окружности равен 12 см.

Чему равен радиус окружности?

d = 12 см

r = d : 2

r = 12 : 2 = 6 (см) радиус окружности

Ответ: r = 6 см

Важно отметить, что все рассмотренные элементы окружности одинаковы и для круга.

Давайте выясним, что такое длина окружности и как ее определить.

Представьте, что окружность обернута нитью.

Если разрезать эту нить в некоторой точке и размотать ее, то длина нитки будет равна длине окружности.

Обычно длина окружности обозначается заглавной буквой С

Длина окружности (С) зависит от длины ее диаметра (d)

Обратите внимание на рисунок.

Вы можете заметить, что чем больше диаметр, тем больше длина окружности.

Из этого следует, что длина окружности прямо пропорционально зависит от диаметра окружности.

А значит, для любых окружностей отношение длины окружности (С) к длине диаметра (d) является числом постоянным.

С– это длина окружности

d– диаметр окружности

отсюда следует, что длина окружности равна

Так как диаметр окружности вдвое больше радиуса d = 2r, получим еще одну формулу для вычисления длины окружности

Мы с вами не будем оперировать настолько точными данными.

Так как круг – это часть плоскости, то одной из его характеристик является площадь.

Где S– это площадь круга

r– радиус круга

Рассмотрим примеры решения задач

Найдите длину окружности, если ее радиус равен 4 см.

r = 4 см

Длину окружности С – ?

Длина окружности надувного бассейна 15,7м.

Найдите диаметр этого бассейна.

C = 15,7 м

Диаметр d – ?

Диаметр окружности равен 6 см.

Найдите площадь круга, ограниченного этой окружностью.

d = 6 cм

Площадь круга S – ?

Подставим в формулу известные значения диаметра окружности и постоянной , получим:

Вычислите площадь полукруга, если радиус круга равен 5 см.

r = 5 cм

Площадь полукруга S_п – ?

Площадь круга найдем по формуле:

Площадь полукруга будет равна половине площади всего круга.

Следовательно, формула для расчета площади полукруга получится вида:

Найдите площадь круга, если известна длина окружности С.

Длина окружности С

Площадь круга S – ?

Длина окружности выражается формулой:

Выразим неизвестный радиус окружности через длину окружности:

Площадь круга определяем по формуле:

Подставим, полученные выражения для радиуса окружности, в формулу площади круга, получим:

Сократим полученную дробь:

–
Саша, чем ты занимаешься? – поинтересовался у друга Паша.

–
Нам по математике задали разгадать ребус, по которому мы узнаем тему нашего
следующего урока, – ответил Саша. — Но я забыл, как разгадываются ребусы.

–
Не расстраивайся! – подбодрил друга Паша. – Я помогу тебе. Показывай свой
ребус.

–
Вот, смотри, какое загадочное слово! – воскликнул Саша.

–
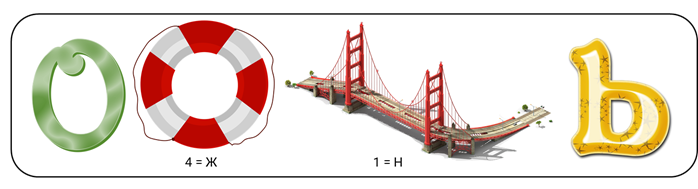
Саша, да это совсем лёгкий ребус, – отметил Паша. – Сейчас мы быстренько всё разгадаем.
Итак, твой ребус начинается с буквы «О». Букву эту и оставим на первом месте. Затем
нарисована картинка, а под ней равенство цифры и буквы. Напомню, что знак
равенства, изображённый возле картинки, служит для обозначения замены одной из
букв на другую. У тебя нарисован круг, а снизу равенство, указывающее, что
нужно четвёртую букву в названии картинки заменить на букву «Ж». Что за слово
получится после замены?

–
Был «круг», заменим четвёртую букву на «Ж», значит, у нас получится «круж», –
сказал Саша.

–
Отлично! – поддержал друга Паша. – Идём дальше. Здесь нарисован мост и снова
под картинкой равенство цифры и буквы. Что за слово получится?

–
В слове «мост» нужно заменить букву «м» на букву «н», – начал размышлять Саша.
– Тогда после замены получим слово «ност».

–
Верно! – согласился Паша. – И заканчивается твой ребус буквой «ь». Эта буква и будет
завершать всё слово. А теперь попробуй из получившихся слов и букв составить
единое слово.

–
Молодец, Саша! – похвалил друга Паша. — Значит, на уроке математики вы будете
знакомиться с окружностью!

–
Интересно, а что же нам про неё расскажут? – спросил Саша.

–
А давай обратимся к Мудряшу, – предложил Паша. – Он точно сможет много интересного
рассказать об этой замечательной геометрической фигуре.

–
Ребята, прежде чем я расскажу вам об окружности и круге, давайте немного
разомнёмся и выполним устные задания, – предложил Мудряш.

–
Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было
получиться!

–
Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Многие предметы нашего
окружения имеют формы, похожие на определённые геометрические фигуры. Давайте
посмотрим на следующие предметы из нашей жизни. Скажите, что их всех
объединяет?

–
Все эти предметы — круглые, – заметил Саша.

–
Правильно! – согласился Мудряш. – А что вы можете сказать об их форме? На какие
геометрические формы они похожи?

–
Кольца, гимнастический обруч и колесо велосипеда имеют форму окружности, – сказал
Паша, – а вот пицца, тарелка и настенные часы – форму круга.

–
Всё верно! – обрадовался Мудряш. – В начальных классах вы уже знакомились с
этими фигурами. Чтобы разобраться, что такое окружность и чем она отличается от
круга, необходимо иметь чёткое представление об этих фигурах. И начнём мы,
пожалуй, разговор с окружности. Итак, вы уже знаете, что окружность легко
начертить с помощью циркуля. Давайте вспомним, как происходит этот процесс.

–
Для того чтобы начертить окружность, мы должны установить остриё циркуля (иглу)
на бумагу, – начали рассказывать мальчишки. – А вторую ножку циркуля, которая с
карандашом, нужно вращать вокруг первой. Карандаш начертит на плоскости листа
линию, которая и называется окружностью.

–
Молодцы! – похвалил ребят Мудряш. – Запомните! Окружность –
это геометрическая фигура на плоскости, все точки которой равноудалены от
данной точки – центра окружности. Точка, в которой устанавливалось остриё
циркуля (игла), называется центром окружности. Как правило, центр
окружности обозначают точкой О.

–
О чём говорит фраза «все точки которой равноудалены от данной точки»? –
спросил у ребят Мудряш.

–
Это значит, что все точки окружности удалены от её центра на одинаковое
расстояние, – ответили мальчишки.

–
Правильно! – согласился Мудряш. – Кстати, именно этот факт позволяет любому
транспортному средству на колёсах ехать ровненько, так как при движении
транспортного средства центр колеса всегда находится на одинаковом расстоянии
от земли.

–
А теперь давайте соединим центр окружности, то есть нашу точку О, с любой
понравившейся вам точкой на окружности, – продолжил Мудряш. – Обозначим эту
точку, например буквой А. Видим, что у нас получился отрезок ОА.

Запомните! Отрезок,
соединяющий центр окружности с любой её точкой, лежащей на окружности, называют
радиусом.

–
А если мы ещё поставим точки на окружности, например В и К, и соединим эти
точки с центром окружности, – решили спросить мальчишки, – отрезки ОВ и ОК тоже
будут радиусами?

–
Верно! – ответил Мудряш. – На нашем рисунке отрезки ОА, ОВ, ОК – радиусы
окружности. Причём все радиусы одной окружности равны между собой. То есть радиусы
ОА, ОВ и ОК равны.

–
Давайте измерим длину нашего радиуса О А, – сказал Мудряш.

–
Эта длина равна 2,5 сантиметра, – померили мальчишки.

–
Хорошо! – продолжил Мудряш. – Говорят, что длина радиуса ОА равна 2,5
сантиметра. Но зачастую слово «длина» не произносят, а вместо «длина радиуса»
говорят просто «радиус». То есть можно сказать, что радиус окружности равен 2,5
сантиметра. Радиус окружности принято обозначать буквой r.
Тогда для нашей окружности можно записать, что r
= 2,5 сантиметра.

–
А теперь давайте отметим любые две точки на окружности, например M
и N, и соединим их отрезком. Видим, что
у нас получился отрезок MN.

Запомните! Отрезок,
соединяющий любые две точки окружности, называют хордой.

–
Отрезок ЕF —
тоже хорда, – ответил Мудряш. – Только у этой хорды есть собственное название.

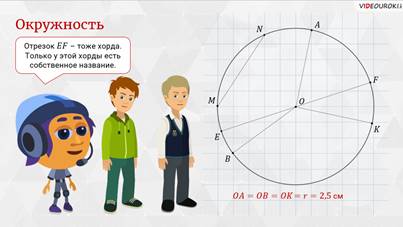
Запомните! Отрезок,
соединяющий две точки на окружности и проходящий через центр окружности, называют
диаметром окружности.

–
Если посмотреть внимательно на диаметр ЕF,
– заметил Паша, – то увидим, что диаметр состоит из 2 радиусов.

–
Ты очень внимательный! – сказал Мудряш. – Диаметр окружности равен двум её
радиусам. Поэтому диаметр в 2 раза больше радиуса. Диаметр окружности принято обозначать
буквой d. Значит, можем записать,
что d =
2r.

–
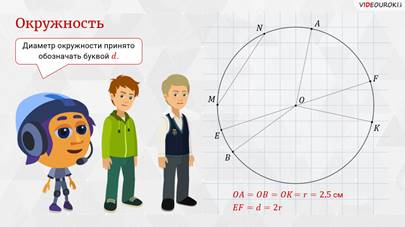
Две точки, лежащие на окружности, например Е и F,
делят её на 2 части, – продолжил Мудряш. – Каждую из этих частей называют дугой
окружности. Точки Е и F
называют концами дуг.

–
Ну, с окружностью всё понятно, – сказал Саша, – а чем же тогда отличается круг
от окружности? Он тоже круглый.

–
Любая окружность разделяет плоскость на две части, – начал Мудряш. – Ту часть
плоскости, которая лежит внутри окружности вместе с самой окружностью, называют
кругом.

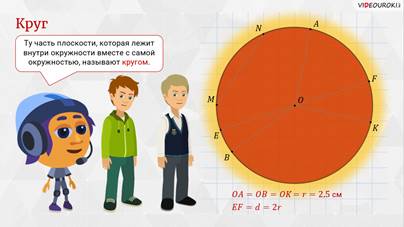
Круг
имеет центр, радиус, диаметр, хорду – это соответственно центр, радиус, диаметр,
хорда окружности, ограничивающей круг. Назовите элементы нашего круга.

–
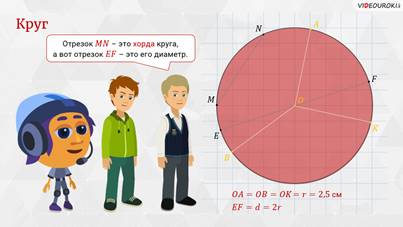
Точка О – это центр круга, – сказал Саша. – Отрезки ОА, ОB
и ОК – его радиусы.

–
Отрезок MN – это хорда нашего круга,
– ответил Паша, – а вот отрезок ЕF
– это его диаметр.

–
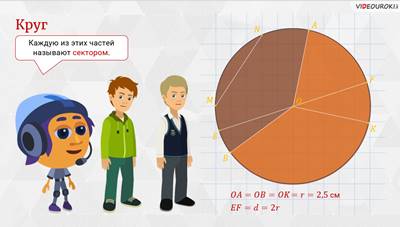
Молодцы! – похвалил ребят Мудряш. – Если из центра О круга провести два радиуса,
например ОА и ОB, то они разделят круг на
две части. Каждую из этих частей называют сектором.

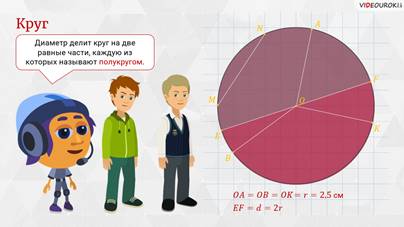
А
что касается нашего диаметра ЕF,
то он делит круг на две равные части, каждую из которых называют полукругом.

–
Несложно догадаться, что точки могут лежать на окружности (мы будем говорить «принадлежат
окружности»), а могут и не лежать на ней, то есть не принадлежать окружности. Аналогично
и с кругом, – продолжил Мудряш. – Например, точки А, B
и К принадлежат окружности с центром в точке О. А точки О, C
и D не принадлежат окружности с центром
в точке О. В свою очередь, точки О, А, B,
К и C принадлежат
кругу с центром в точке О. А вот точка D
не принадлежит этому кругу. При этом точка D
удалена от центра круга на расстояние, большее радиуса.

Запомните! Если
точка удалена от центра круга на расстояние, меньшее радиуса круга или равное
ему, то эта точка принадлежит кругу.

–
А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько
заданий.

Задание
первое: начертите окружность радиусом 2 сантиметра с центром
в точке О. Вычислите диаметр этой окружности.

Решение: при
помощи линейки сделаем раствор циркуля равным 2 сантиметрам. Ножку с иголкой
поместим в точку О, а ножкой с карандашом опишем окружность. А теперь вычислим
диаметр нашей окружности. Так как диаметр в 2 раза больше радиуса, то диаметр
нашей окружности равен 4 сантиметрам.

Задание
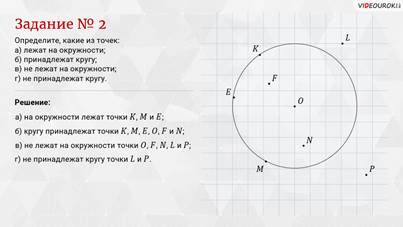
второе: определите, какие из точек лежат на окружности,
принадлежат кругу, не лежат на окружности, не принадлежат кругу.

Решение: на
окружности лежат точки К, M
и Е. Кругу принадлежат точки К, M,
Е, О, F и N.
Не лежат на окружности точки О, F,
N, L
и P. Не принадлежат кругу точки L
и P.

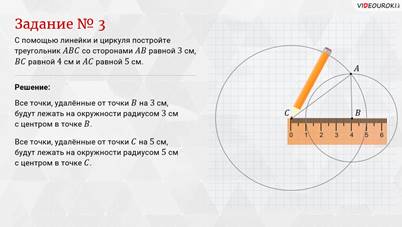
И
последнее задание: с помощью линейки и циркуля постройте
треугольник АBC со сторонами АB
равной 3 сантиметрам, BC
равной 4 сантиметрам и АC
равной 5 сантиметрам.

Решение:
с помощью линейки построим отрезок CB
длиной 4 сантиметра. Третья вершина А треугольника должна быть удалена от точки
B на 3 сантиметра, а от точки C
– на 5 сантиметров. Все точки, удалённые от точки B
на 3 сантиметра, будут лежать на окружности радиусом 3 сантиметра с центром в
точке B. Построим эту
окружность. Все точки, удалённые от точки C
на 5 сантиметров, будут лежать на окружности радиусом 5 сантиметров с центром в
точке C. Построим вторую
окружность. Следовательно, точка А будет точкой пересечения этих окружностей. Соединим
точку А с точками B и C.
Мы получили искомый треугольник АBC.

МБОУ «Апраксинская СОШ»

Урок по математике, 6 класс

“Длина окружности и площадь круга”

Подготовила и провела:        

 «Длина окружности и площадь круга».

 сформировать представления о длине окружности и площади круга, познакомить с формулами вычисления длины окружности и площади круга.

• изучить формулы длины окружности и площади круга;
• показать их применение при решении задач;
• познакомить с числом
• прививать учащимся навык самостоятельности в работе, учить трудолюбию, аккуратности.

• развивать познавательный интерес учащихся в процессе ознакомления с историческим материалом;
• развивать навык устного счёта;
• развивать мыслительную деятельность учащихся;
• развивать пространственное воображение учащихся.

• воспитывать интерес к математике;
• воспитывать умение работать с имеющейся информацией;
• воспитывать умение видеть математические задачи в окружающем нас мире.

Урок формирования новых знаний.

Оборудование и наглядность:

• компьютер, проектор, экран;
• рабочий лист, модели окружности и круга, нитка, линейка.

1. Орг. момент.

2. Вступительное слово учителя.

3. Изучение нового материала.

4. Практическая работа.

5. Историческая справка.

6. Умная физкультминутка.

7. Самостоятельная работа.

8. Итог урока.

9. Домашнее задание.

I. Орг. момент.

Истина не рождается в голове отдельного человека, она рождается между людьми совместно ищущими, в процессе их диалогического общения.                Бахтин М.М.

Сообщение темы и цели урока.        «Длина окружности и площадь круга».

А такие предметы, как: кольца, браслеты, обручи, бублики?                (окружность)

II. Изучение нового материала.

1. Работа по готовому чертежу.

• Какая геометрическая фигура изображена на чертеже?        (окружность)
• Что такое окружность?                (Определение. Окружность – это замкнутая линия, все точки которой находятся на равном расстоянии от данной точки плоскости, называемой центром.
• Назовите центр окружности?                (точка О – точка внутри круга, от которой равноудалены все точки окружности, называется – центром окружности).
• Какой отрезок называется радиусом?        (ОD=r – радиус окружности – это отрезок, соединяющий центр окружности с любой её точкой) (Радиус – от латинского слова – луч, спица в колесе)
• Какой отрезок называется хордой окружности?        (АВ – хорда окружности – это отрезок, соединяющий любые две точки на окружности; хорда разбивает окружность на две части, которые называются – дугами окружности).
• Какой отрезок называют диаметром?        (ВС=d – диаметр окружности – это хорда, проходящая через центр окружности; диаметр – это наибольшая из хорд окружности). (Диаметр – от латинского слова – поперечник, насквозь измеряющий).
• Во сколько раз диаметр длиннее радиуса?        ( в два раза; диаметр и радиус связаны формулой: d=2r)
• Есть ли у окружности два радиуса различной длины?
• Два диаметра различной длины?
• Если окружность заштриховать, то какая фигура получится?

 – удивительно гармоничная фигура, древние греки считали её самой совершенной, т.к. окружность – единственная кривая, которая может «скользить сама по себе», вращаясь вокруг центра. Основное свойство окружности даёт ответ на вопросы, почему для её вычерчивания используют циркуль и почему колеса делают круглыми, а не квадратными. Колесо – одно из самых великих изобретений человечества.

Окружность можно начертить с помощью циркуля (циркуль – от латинского слова – круг). Для этого надо:

1. Отметить точку на плоскости.

2. Ножку циркуля с остриём совместить с отмеченной точкой, а ножкой с грифелем вращать вокруг этой точки.

3. Получилась геометрическая фигура – окружность.

 Начертите окружность, укажите центр окружности, её радиус, диаметр, хорду. Сделайте соответствующие обозначения. Измерьте длину радиуса и диаметр окружности. Сделайте вывод.

Запишите в тетрадях

После выполнения упражнения, в тетрадях должна получиться запись:

ОР, ОУ, КН, СЖ, ТЬ   //  РУ, АД, СИ  //  РУ, ГК.

Ребята, сегодня на уроке мы с вами будем устанавливать экспериментальным путём зависимость между диаметром и длиной окружности; зависимость между площадью круга и его радиусом. Для этого вы выполните

5. Практическая работа по теме «Длина окружности и площадь круга»

 вывести формулу зависимости между диаметром и длиной окружности;

установить зависимость между площадью круга и его радиусом.

. Поставьте цилиндр на лист бумаги и обведите его карандашом.

 На бумаге получится замкнутая кривая линия – окружность. Укажите её центр и проведите диаметр.

 «Опояшем» цилиндр ниткой (один раз) так, чтобы конец нитки совпал с началом в одной и той же точке окружности, оставшуюся часть нитки отрежьте.

 Выпрями эту нитку и по линейке измерь её длину, это и будет длина окружности. Длину окружности обозначают буквой С.

 Измерьте диаметр основания цилиндра (диаметр окружности). Обозначив его буквой d, запишите, чему равен диаметр d.

 Вычислите отношение длины окружности к диаметру (с точностью до сотых).

Для всех окружностей отношение длины окружности к длине её диаметра является одним и тем же числом  – это греческая буква (пи).

 А теперь посмотрите на окружность своей клетчатой бумаги. Посчитайте, сколько полных квадратиков внутри круга. Найдите приближенно площадь круга.

Отношение площади круга к квадрату радиуса является одним и тем же числом

Историческая справка (о числе пи)

 – бесконечная десятичная дробь. Обозначение числа происходит от первой буквы греческого слова периферия, что означает «окружность». Общепринятым это обозначение стало, после издания одной из работ Эйлера. На ранних ступенях человеческого развития пользовались неточным числом . Оно было равно 3.

Египетские и римские математики установили отношение длины окружности к диаметру не строгим геометрическим расчётом, как позднейшие математики, а нашли его просто из опыта.

Многие учёные-математики пытались доказать, что это отношение есть число постоянное, не зависящее от размеров окружности. Впервые это удалось сделать древнегреческому математику Архимеду. Он нашёл довольно точное значение этого отношения. Архимед жил на Сицилии с 287г до 212г до н.э. Используя рассуждение, он доказал, что

На самом деле число  не может быть выражено точной дробью. Математик 16 века Лудольф имел терпение вычислить его с 35 десятичными знаками. В 1946-1947гг два ученых независимо друг от друга вычислили 808 десятичных знаков числа

Малоизвестный математик Шенкс опубликовал такое значение числа , в котором после запятой следовало 707 десятичных знаков, но, начиная с 528-го знака, он ошибся.

Такие длинные числа, приближённо выражающие значение числа , не имеют ни практической, ни теоретической ценности. Для обычных вычислений с числом  вполне достаточно запомнить два знака после запятой (3.14).

III. «Умная физкультминутка». Снять утомление, обеспечить активный отдых и повысить умственную работоспособность обучающихся.

Если вы со мной согласны – поднимите руки вверх и опустите их вниз. Если – нет, то выполните повороты корпуса вправо и влево.

1) По формуле С=2R можно вычислить длину окружности?                        (да)

2) Диаметром окружности называется отрезок, соединяющий две точки окружности.

3) Буквой С обозначают площадь круга?                                                        (нет)

4) По формуле S= можно вычислить площадь круга?                                (да)

5) Часть плоскости, ограниченная окружностью, называется кругом.                (да)

7) По формуле С = d можно вычислить длину окружности?                        (нет)

IV. Закрепление знаний учащихся по данной теме.

а) Найди пару

V. Решение задач.

 R= 6370км.                С – ?

Решение:                С = 2r,   С

. Отлитый в 1735г. Царь колокол, хранящийся в Московском Кремле, имеет диаметр основания 6,6м. Вычислите площадь окружности основания Царь-колокола.

 А сейчас я приглашаю вас в цирк. Внимание аттракцион: «Бегемот Пумпа на велосипеде». Пумба совершает один круг по арене за 3 минуты. Если едет со скоростью 13.5 м/мин. каков диаметр арены?

Решение:                13,5*3=40,5м – путь.  С =,   d = С :  

VI. Подведение итогов урока. Рефлексия.

• Ты доволен тем, как прошёл урок?
• Тебе было интересно?
• Сумел ли ты получить новые знания?
• Ты сумел показать свои знания?

• Что нового вы узнали на уроке?
• Что показалось наиболее интересным?

        п. 24(с.137-138);                №8697, №870, 873(в,г).

Построение окружности

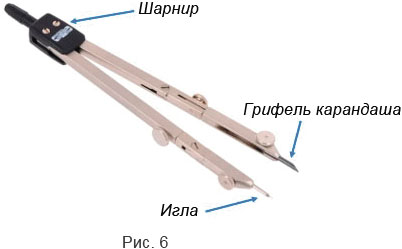
Для того, чтобы построить окружность используют специальный прибор, который называется циркулем (Рис.6). Циркуль состоит из двух частей, соединённых шарниром. Обычно на конце одной из них располагается игла, на конце другой — пишущий предмет, например грифель карандаша.

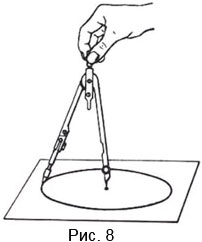
• отмечаем точку, которая будет центром окружности;
• делаем нужный раствор циркуля (расстояние между иглой и грифелем карандаша), т.е. определяем радиус окружности, которую нам нужно построить (Рис.7);

• ставим иглу циркуля в точку, которая определяет центр окружности;
• проводим окружность данного радиуса (Рис.8).

Часть плоскости, которая лежит внутри окружности (вместе с самой окружностью), называют кругом (Рис.9).

Шар и сфера

Сфера – поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

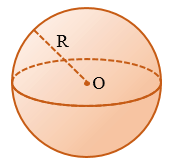
Центр сферы – данная точка (точка О на рисунке выше).

Радиус сферы – данное расстояние (R на рисунке выше), также это любой отрезок, соединяющий центр сферы с какой-либо ее точкой.

Диаметр сферы – отрезок, соединяющий две точки сферы и проходящий через ее центр. Диаметр сферы в два раза больше ее радиуса, т.е. если радиус сферы – R, то ее диаметр – 2R.

Определение

Шар – тело, ограниченное сферой.

Правило встречается в следующих упражнениях

Задание 852,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 856,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 876,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 914,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 920,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 963,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1662,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1707,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1811,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1847,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 715,
Мерзляк, Полонский, Якир, Учебник

Номер 718,
Мерзляк, Полонский, Якир, Учебник

Номер 735,
Мерзляк, Полонский, Якир, Учебник

Номер 3,
Мерзляк, Полонский, Якир, Учебник

Номер 5,
Мерзляк, Полонский, Якир, Учебник

Номер 6,
Мерзляк, Полонский, Якир, Учебник

Номер 2,
Мерзляк, Полонский, Якир, Учебник

Задание 856,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1054,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1536,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 19,
Мерзляк, Полонский, Якир, Учебник

Номер 20,
Мерзляк, Полонский, Якир, Учебник

Номер 1225,
Мерзляк, Полонский, Якир, Учебник

Советуем посмотреть

Единицы измерения площадей. Свойства площадей

Прямоугольник, его периметр и площадь. Ось симметрии фигуры

Квадрат. Периметр и площадь квадрата.

Многоугольники. Правильные многоугольники. Равенство фигур.

Шкалы и координаты

Прямоугольный параллелепипед. Пирамида.

Объем прямоугольного параллелепипеда

Куб. Площадь поверхности куба

Куб. Объем куба

Угол. Обозначение углов

Прямой и развернутый угол

Измерение углов. Транспортир. Виды углов

Треугольник и его виды