В пространстве есть два смежных секущих прямых угла. Если они не пересекаются, то параллельны и перпендикулярны

Геометрия. 7 класс

Свойства параллельных прямых

Перечень рассматриваемых вопросов:

• Углы, образованные при пересечении двух прямых секущей.
• Доказательство свойств параллельных прямых и их применение при решении задач.
• Формулирование теоремы об углах с соответственно параллельными сторонами.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Утверждение, обратное данной теореме– это утверждение, в котором условие является заключением теоремы, а заключение – условием теоремы.

• Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
• Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
• Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
• Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
• Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Ранее мы узнали и научились применять признаки параллельности прямых.

Рассмотрим утверждения, обратные к теоремам, выражающим признаки параллельности двух прямых.

В любой теореме есть две части: условие (это то, что дано)и заключение (это то, что требуется доказать).

Утверждением, обратным данному, называется утверждение, в котором условием является заключение, а заключением – условие.

Итак, вспомним один из признаков параллельности прямых. Если при пересечении двух прямых секущей накрест лежащие углы, образованные этими прямыми и секущей, равны (это условие), то прямые параллельны (заключение).

Сформулируем и докажем обратное утверждение.

Если две параллельные прямые пересечены секущей, то накрест лежащие углы,образованные этими прямыми и секущей,равны.

∠1 и ∠2 – накрест лежащие.

Доказательство:( метод от противного):

Это противоречит теореме о единственности прямой параллельной данной и проходящей через точку.

Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.

Что и требовалось доказать.

Вспомним ещё один признак параллельности двух прямых. Если при пересечении двух прямых секущей соответственные углы равны(это условие), то прямые параллельны(заключение).

Если две параллельные прямые пересечены секущей, то соответственные углы, образованные этими прямыми и секущей, равны.

Значит, ∠1 = ∠2, что и требовалось доказать.

Вспомним ещё один признак параллельности двух прямых. Если при пересечении двух прямых секущей сумма односторонних углов, образованных этими прямыми и секущей, равна 180° (условие), то прямые параллельны (заключение).

Если две параллельные прямые пересечены секущей, то сумма односторонних углов, образованных этими прямыми и секущей, равна 180°.

∠2+∠4=180° (по свойству смежных углов).

Материал для углубленного изучения темы.

Задача на доказательство.

Прямая m пересекает параллельные прямые а и b в точках А и В. Прямая р, проходящая через середину отрезка АВ, точку О, пересекает прямые а и b в точках С и D.

Докажем, что ОС=ОD.

По условию дано: а ║b, рՈа= А, рՈb = В, mՈа = D, mՈb = C.

Доказать: ОС = ОD.

Разбор заданий тренировочного модуля.

1. Три прямых а,р,с пересечены прямой k, при этом образуются соответственные углы: ∠1= 30°,∠2 = 40°,∠3= 30°,как показано на рисунке. Какие из прямых параллельны?

На рисунке изображены прямые а, р, с, которые пересечены секущей k. При этом углы 1,2,3 соответственные. По условию: ∠3= ∠1= 30°,∠2 ≠ ∠1,∠2 ≠ ∠3.

Следовательно, прямые а и р параллельные, прямые а и с, р и с не параллельные(по свойствам параллельных прямых).

2. На рисунке прямые а║b, при этомMO и ЕО – биссектрисы углов М и Е соответственно, пересекаются в точке О. Чему равна градусная мера угла МОЕ, если сумма углов в треугольнике равна 180°?

∠М+∠Е =2∠ОМЕ +2∠МЕО =180°.

Теоремы об углах, образованных двумя параллельными прямыми и секущей презентация к уроку по геометрии (7 класс)

Теоремы об углах,образованных двумя параллельными прямыми и секущей

Скачать

Бесплатный марафон подготовки к ЕГЭ на зимних каникулах

Учи.Дома запускает бесплатный марафон в котором каждый день. В течении 5 дней утром ты будешь получать одно задание по выбранному предмету, а вечером его решение. Твоя задача, успеть выполнение задание до того как получишь ответ.

Бесплатно, онлайн, подготовка к ЕГЭ

Предварительный просмотр

Классная работа 15.01.19

Как называются углы при прямых m и l и секущей h ?

Если при пересечении двух прямых секущей соответственные углы равны , то прямые параллельны. Если при пересечении двух прямых секущей сумма односторонних углов равна 180 0 , то прямые параллельны. 1 2 а b c c а b 1 2 c а b 1 2 Если при пересечении двух прямых секущей накрест лежащие углы равны , то прямые параллельны. Признаки параллельности прямых

Аксиома параллельных прямых

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. Следствие 1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую . a II b , c ∩ b ⇒ c ∩ a а А Следствие 2. Если две прямые параллельны третьей прямой, то они параллельны. a II с , b II с ⇒ a II b а b с c b

Теоремы об углах, образованных двумя параллельными прямыми и секущей

1 2 b а c 3 Дано: а II b, c- секущая. Доказать: O У 1 + 2=180 0 . Доказательство: 3+ 2 =180 0 , т. к. они смежные. 1= 3, т. к. это НЛУ при а II b 3 + 2 =180 0 1 Теорема доказана. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 0 .

1 2 b а c 3 Дано: а II b, c- секущая. Доказать: СУ 1 = 2. Доказательство: 2 = 3, т. к. они вертикальные. 3 = 1, т. к. это НЛУ при а II b 1 = 3 = 2 Теорема доказана. 1 2 Если две параллельные прямые пересечены секущей, соответственные углы равны.

a b 34 0 1 a b 2 1 1 + 2 = 76 0 . a b 136 1 44 0 44 0 a II b a II b 2 2 3 a b 1 34 0 2 a II b 1: 2 = 4 : 5. a b 1 a II b 1 2 a II b № 1 № 2 № 3 № 4 № 5 с с с с с d

Домашнее задание: стр. 58 – 63, учить аксиомы, теоремы и их доказательства; решить задачи № 201, 202, 205.

Используя данные рисунка, найдите углы 1, 2 и 3. а b с d 20 0 120 0 160 0 1 2 3

Может ли еще один из семи остальных углов, образованных при пересечении прямых a и b с прямой d , быть равен 110 0 ? 60 0 ? Почему? а b m d 11 0 0 4 0 0 4 0 0 4 0 0 11 0 0 11 0 0 11 0 0

Тренировочные упражнения 2 1 b а c Дано: а II b , с – секущая 1 = 4 2 Найдите: 1 и 2 Угол 1 в 4 раза больше угла 2 х 4х

Тренировочные упражнения 2 1 b а c Дано: а II b , с – секущая 1 – 2 = 30 0 Найдите: 1 и 2 х х+30 b а c Угол 1 на 30 0 больше угла 2

Тренировочные упражнения 2 1 b а c Дано: а II b , с – секущая 2 = 0,8 1 Найдите: 1 и 2 Угол 2 составляет 0,8 части угла 1 х 0,8х

Тренировочные упражнения 2 1 b а c Дано: а II b , с – секущая 1 : 2 = 5 : 4 Найдите: 1 и 2 5х 4х 5 : 4 Пусть х – 1 часть

% Тренировочные упражнения 2 1 b а c Дано: а II b , с – секущая 2 составляет 80% от 1 Найдите: 1 и 2 х 0,8х

2 1 b а c Дано: а II b , с – секущая 1 : 2 = 5 : 4 Найдите: 1 и 2 5х 4х AB = BC, A=60 0 , CD – биссектриса угла ВСЕ. Докажите, что АВ II CD . A С B D E 60 0 60 0 120 0 60 0 60 0 биссектриса 5 : 4 Пусть х – 1 часть

На рисунке АС II В D и АС = АВ, МАС = 40 0 . Найдите СВ D. С D M A 40 0 2 1 3 B

4 3 2 1 E D A Построим CN II AB B На рисунке АВ II Е D . Докажите, что ВС D = B + D C Подсказка N

E D A Построим CN II AB B C Подсказка N 140 0 130 0 40 0 50 0 На рисунке АВ II Е D . C ВА = 140 0 , С DE = 130 0 Докажите, что ВС С D

6 4 5 На рисунке a II b , c – секущая, DM и DN – биссектрисы смежных углов, образованных прямыми a и c . DE = 5 ,8 см Найдите MN. с D M 40 0 2 1 3 E а b N 5 ,8 см ?

A D E 3 4 0 B C M На рисунке АВ ED и KM ED, ABE = 34 0 MN – биссектриса КМС Найдите EMN. K 146 0 3 4 0 73 0 73 0 ? N

A D E 48 0 B C M На рисунке АС II BD и KC II MD, ACK = 48 0 CDK в 3 раза больше EDM Найдите К DE. K 48 0 48 0 x 3x

«Управление общеобразовательной организацией

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Теоремы об углах, образованных двумя параллельными прямыми и секущей.

Теорема: Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны. а в А В 1 2  1 =  2 c

Доказательство: A B C D M N 1 2 A B C D M N 1 2 K O Пусть прямые АВ и СD параллельны, МN — их секущая. Докажем, что накрест лежащие углы 1 и 2 равны между собой. Допустим, что  1 и  2 не равны. Проведем через точку О прямую КF. Тогда при точке О можно построить  KON, накрест лежащий и равный  2. Но если  KON =  2, то прямая КF будет параллельна СD. Получили, что через точку О проведены две прямые АВ и КF, параллельные прямой СD. Но этого не может быть. Мы пришли к противоречию, потому что допустили, что  1 и  2 не равны. Следовательно, наше допущение является неправильным и  1 должен быть равен  2, т. е. накрест лежащие углы равны. F

Теорема: Если две параллельные прямые пересечены секущей, то соответственные углы равны. а в А В 1 2  1 =  2

Доказательство: 2 а в А В 3 1 Пусть параллельные прямые а и b пересечены секущей АВ, то накрест лежащие  1 и  3 будут равны.  2 и  3 равны как вертикальные. Из равенств 1 = 3 и 2 = 3 следует, что 1 = 2. Теорема доказана

Теорема: Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°. а в А В 3 1  1 +  3 = 180°

Доказательство: Пусть параллельные прямые а и b пересечены секущей АВ, то соответственные  1 и  2 будут равны,  2 и  3 – смежные, поэтому  2 +  3 = 180°. Из равенств 1 = 2 и 2 + 3 = 180° следует, что 1 + 3 = 180°. Теорема доказана. 2 а в А В 3 1

Решение: 1. Пусть Х – это  2, тогда  1 = (Х+70°), т.к. сумма углов 1 и 2 = 180°, в силу того, что они смежные. Составим уравнение: Х+ (Х+70°) = 180° 2Х = 110 ° Х = 55° (Угол 2) 2. Найдем  1. 55° + 70° = 125° 3.  1 =  3, т.к. они вертикальные.  3 =  5, т.к. они накрест лежащие. 125°  5 =  7, т.к. они вертикальные.  2 =  4, т.к. они вертикальные.  4 =  6, т.к. они накрест лежащие. 55°  6 =  8, т.к. они вертикальные. Задача №1: A B 4 3 5 8 7 2 1 6 Условие: найдите все углы, образованные при пересечении двух параллельных A и B секущей C, если один из углов на 70° больше другого.

Решение: 1. Т.к. 4 = 45°, то2 = 45°, потому что 2 =4(как соответственные) 2.  3 смежен с  4, поэтому 3+4=180°, и из этого следует, что 3= 180° — 45°= 135°. 3.  1 =  3, т.к. они накрест лежащие.  1 = 135°. Ответ:  1=135°;  2=45°;  3=135°. Задача №2: A B 1 Условие: на рисунке прямые А II B и C II D,  4=45°. Найти углы 1, 2, 3. 3 2 4

Решение: 1. 1=2, т.к. они вертикальные, значит 2= 45°. 2.  3 смежен с  2, поэтому 3+2=180°, и из этого следует, что 3= 180° — 45°= 135°. 3.  4 + 3=180°, т.к. они односторонние.  4 = 45°. Ответ:  4=45°;  3=135°. Задача №3: A B 2 Условие: две параллельные прямые А и B пересечены секущей С. Найти, чему будут равны 4 и 3, если 1=45°. 3 4 1

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: 78254042147

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов

Во всех педвузах страны появятся технопарки

В Минпросвещения рассказали о формате обучения школьников после праздников

Минпросвещения создает цифровую психологическую службу для школьников

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Статья рассматривает понятия параллельность прямой  и плоскости. Будут рассмотрены основные определения и приведены примеры.  Рассмотрим признак параллельности прямой к плоскости с необходимыми и достаточными условиями параллельности, подробно решим примеры заданий.

Параллельные прямые и плоскость – основные сведения

Прямая и плоскость называются параллельными, если не имеют общих точек, то есть не пересекаются.

Параллельность обозначается «∥». Если в задании по условию прямая a и плоскость α параллельны, тогда обозначение имеет вид a∥α. Рассмотрим рисунок, приведенный ниже.

Считается, что прямая a, параллельная плоскости α и плоскость α, параллельная прямой a, равнозначные, то есть прямая и плоскость параллельны друг другу в любом случае.

Параллельность прямой и плоскости – признак и условия параллельности

Не всегда очевидно, что прямая и плоскость параллельны. Зачастую это нужно доказать. Необходимо использовать достаточное условие, которое даст гарантию на параллельность. Такой признак имеет название признака параллельности прямой и плоскости. Предварительно рекомендуется изучить определение параллельных прямых.

Если заданная прямая a, не лежащая в плоскости α, параллельна прямой b, которая принадлежит плоскости α, тогда прямая a параллельна плоскости α.

Рассмотрим теорему, используемую для установки параллельности прямой с плоскостью.

Если одна из двух параллельных прямых параллельна плоскости, то другая прямая лежит в этой плоскости либо параллельна ей.

Подробное доказательство рассмотрено в учебнике 10-11 класса по геометрии. Необходимым и достаточным условием параллельности прямой с плоскостью возможно при наличии определения направляющего вектора прямой и нормального вектора плоскости.

Для параллельности прямой a, не принадлежащей плоскости α, и данной плоскости необходимым и достаточным условием является перпендикулярность направляющего вектора прямой с нормальным вектором заданной плоскости.

Условие применимо, когда необходимо доказать параллельность в прямоугольной системе координат трехмерного пространства. Рассмотрим подробное доказательство.

Допустим, прямая а в систему координат Оху задается каноническими уравнениями прямой в пространстве , которые имеют вид x-x1ax=y-y1ay=z-z1az или параметрическими уравнениями прямой в пространстве x=x1+ax·λy=y1+ay·λz=z1+az·λ, плоскостью α с общими уравнениями плоскости Ax+By+Cz+D=0.

Определить, параллельны ли прямая x=1+2·λy=-2+3·λz=2-4·λ с плоскостью x+6y+5z+4=0.

Получаем, что предоставленная прямая не принадлежит плоскости, так как координаты прямой M(1, -2, 2) не подходят. При подстановке получаем, что 1+6·(-2)+5·2+4=0⇔3=0.

Ответ: прямая с плоскостью параллельны.

Определить параллельность прямой АВ в координатной плоскости Оуz, когда даны координаты A(2, 3, 0), B(4, -1, -7).

Отсюда следует, что прямая АВ с координатной плоскостью Оyz не являются параллельными.

Ответ: не параллельны.

Не всегда заданное условие способствует легкому определению доказательства параллельности прямой  и плоскости. Появляется необходимость в проверке принадлежности прямой a плоскости α. Существует еще одно достаточное условие, при помощи которого доказывается параллельность.

При заданной прямой a  с помощью уравнения  двух пересекающихся плоскостей A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0, плоскостью α – общим уравнением плоскости  Ax+By+Cz+D=0.

Необходимым и достаточным условием для параллельности прямой a и плоскости α яляется отсутствие решений системы линейных уравнений, имеющей вид A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0Ax+By+Cz+D=0.

Из определения следует, что прямая a с плоскостью α не должна иметь общих точек, то есть не пересекаться, только в этом случае они будут считаться параллельными. Значит, система координат Охуz не должна иметь точек, принадлежащих ей и удовлетворяющих всем уравнениям:

A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0, а также уравнению плоскости Ax+By+Cz+D=0.

Следовательно, система уравнений, имеющая вид A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0Ax+By+Cz+D=0, называется несовместной.

Верно обратное: при отсутствии решений системы A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0Ax+By+Cz+D=0 не существует точек в Охуz, удовлетворяющих всем заданным уравнениям одновременно. Получаем, что нет такой точки с координатами, которая могла бы сразу быть решениями всех уравнений A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 и уравнения Ax+By+Cz+D=0. Значит, имеем параллельность прямой и плоскости, так как отсутствуют их точки пересечения.

Система уравнений A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0Ax+By+Cz+D=0 не имеет решения, когда ранг основной матрицы меньше ранга расширенной. Это проверяется теоремой Кронекера-Капелли для решения линейных уравнений. Можно применять метод Гаусса для определения ее несовместимости.

Доказать , что прямая x-1=y+2-1=z3 параллельна плоскости 6x-5y+13z-23=0.

Для решения данного примера следует переходить от канонического уравнения прямой к виду уравнения двух пересекающихся плоскостей. Запишем это так:

Чтобы доказать параллельность заданной прямой x-y-2=03x+z=0 с плоскостью 6x-5y+13z-23=0 , необходимо уравнения преобразовать в систему уравнений x-y-2=03x+z=06x-5y+13z-23=0.

Видим, что она не решаема, значит прибегнем к методу Гаусса.

Расписав уравнения, получаем, что 1-10230106-51323~1-102031-60113-1113~1-102031-6000-913.

Отсюда делаем вывод, что система уравнений является несовместной, так как прямая и плоскость не пересекаются, то есть не имеют общих точек.

Делаем вывод, что прямая x-1=y+2-1=z3 и плоскость 6x-5y+13z-23=0 параллельны, так как было выполнено необходимое и достаточное условие для параллельности плоскости с заданной прямой.

Ответ: прямая и плоскость параллельны.

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Признаки параллельности прямых

Определение. Две прямые на плоскости называются параллельными, если они не пересекаются (не имеют ни одной общей точки).

Прямая называется секущей по отношению к прямым, если она пересекает их в двух точках.

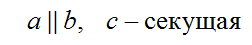
При пересечении прямых секущей образуется восемь углов. Некоторые пары этих углов имеют специальные названия.

Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Теорема 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.

Справедливы обратные теоремы:

Теорема 1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Теорема 2. Если две параллельные прямые пересечены секущей, то соответственные углы равны.

Теорема 3. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 1800.

Аксиома параллельных прямых. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Следствие 1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Прямая и плоскость в пространстве

Параллельность прямой и плоскости

В пространстве прямая может лежать в плоскости, а может и не лежать в ней. При этом, если прямая не лежит в плоскости, то по аксиоме прямой и плоскости она не может иметь с этой плоскостью более одной общей точки. Это означает, что плоскость и не лежащая в ней прямая либо имеют одну общую точку, либо не имеют ни одной общей точки. Если прямая и плоскость имеют ровно одну общую точку, то они пересекаются. А если прямая и плоскость не имеют ни одной общей точки?

ость, не имеющие общей точки, называются параллельными.

Если прямая  и плоскость  параллельны, то записывают    или   . При этом говорят, что прямая  параллельна плоскости  или плоскость  параллельна прямой .

При решении стереометрических задач обоснование параллельности прямой и плоскости при помощи только одного определения их параллельности часто затруднительно и не приводит к желаемому результату. В таких случаях пользуются признаками параллельности прямой и плоскости, один из которых выражает следующая теорема.

,   ,   (рис. 50).

Так как прямая  лежит в плоскости , то (по теореме о двух параллельных прямых, одна из которых пересекает плоскость (т. 5)) прямая , параллельная прямой , не может пересекать плоскость ; а так как прямая  по условию не лежит в плоскости , то прямая  параллельна плоскости . Теорема доказана.

Из этой теоремы, в частности, вытекает факт существования и способ построения прямой, параллельной данной плоскости и проходящей через данную точку, не лежащую в этой плоскости.

,  ,    =  (рис. 51).

Прямые  и лежат в одной плоскости . Кроме того, прямая не имеет общих точек с прямой , так как прямая  по условию параллельна плоскости , в которой лежит прямая . Таким образом, прямые  и  лежат в одной плоскости и не имеют общих точек, следовательно, они параллельны по определению. Теорема доказана.

Из этой теоремы, в частности, следует, что если прямая параллельна плоскости , то в плоскости  существует прямая, параллельная прямой , и таких прямых в плоскости бесконечно много.

,  ,  ,    =  (рис. 52).

Докажем, что прямая  параллельна прямой .

По условию теоремы прямая  параллельна прямой , лежащей в плоскости , а значит (по признаку параллельности прямой и плоскости), прямая  параллельна и самой плоскости . Кроме того, плоскость  проходит через прямую  и пересекает плоскость  по прямой . По теореме 10 прямые  и параллельны. Тогда на основании свойства транзитивности параллельности прямых прямая  параллельна прямой . Теорема доказана.

Докажите самостоятельно ещё один признак параллельности прямой и плоскости.

Плоскость и не лежащая в ней прямая, параллельные некоторой прямой, параллельны.

= ,   ,    (рис. 53).

По следствию из теоремы 10 в плоскостях  и  существуют соответственно прямые  и , параллельные прямой , а следовательно, параллельные между собой. Тогда по теореме 11 прямые  и  параллельны прямой  пересечения плоскостей  и . На основании транзитивности параллельности прямых прямая  параллельна прямой . Теорема доказана.

Даны две скрещивающиеся прямые  и . Через каждую точку прямой  проводится прямая, параллельная прямой . Доказать, что все такие прямые лежат в одной плоскости. Как расположена эта плоскость по отношению к прямой ? Ответ обосновать.

Отметим на прямой  произвольную точку и проведём через неё прямую  (единственную!), параллельную прямой . Через пересекающиеся прямые  и  проводим плоскость (единственную!). Обозначим её  (рис. 54). Эта плоскость (по признаку параллельности прямой и плоскости) параллельна прямой .

Пусть  — произвольная точка прямой ,  — прямая, проходящая через точку параллельно прямой . Тогда прямая  параллельна прямой  (т. 7) и лежит в плоскости  (почему?). В силу произвольного выбора точки на прямой  можно сделать вывод: все прямые пространства, параллельные прямой  и пересекающие прямую , лежат в плоскости, которая проходит через прямую  и параллельна прямой .

Самостоятельно докажите единственность плоскости .

Как мы выяснили на прошлом уроке, прямая, пересекающая данную прямую, пересечет также прямую, параллельную данной. Это следствие из аксиомы параллельности открывает нам возможность сформулировать конкретные признаки параллельности прямых, по которым можно доказательно заключать о параллельности тех или иных прямых. Вы все правильно поняли: от аксиом мы наконец переходим к теоремам.

Что такое секущая

Даны прямые $a$ и $b$, параллельные друг другу, и прямая $c$, которая пересекает данные прямые в двух точках.

Подобная прямая, пересекающая две прочие прямые, в геометрии называется секущей. Секущая может проводиться как по отношению к параллельным прямым, так и к непараллельным.

Секущая — прямая пересекающая две прямые, лежащие в одной плоскости, в двух разных точках.

Обращаем внимание на углы при секущей: секущая при пересечении с параллельными прямыми образует восемь углов, которые на чертеже обозначены заглавными латинскими буквами: A, B, C и так далее. Некоторые пары углов при секущей настолько важны, что за ними даже закреплены отдельные названия:

Внутренние и внешние углы при секущей

Внутренние углы при секущей — это углы, которые находятся в общих для прямых полуплоскостях. Однако секущая также образует и внешние углы — те, что располагаются в не пересекающихся полуплоскостях прямых. Посмотрите на чертежи: для наглядности «зоны» внутренних и внешних углов выделены цветом.

Примечательно, что соответственные углы — это пары, состоящие из одного внутреннего и одного внешнего угла. А при должном внимании вы могли догадаться, что накрест лежащие и односторонние углы были выше нами указаны только для внутренней «зоны». Аналогичные пары вообще-то имеются и во внешней «зоне».

Очевидно, что проведение секущей — это специальный геометрический метод для определения параллельности прямых. По тому, являются ли те или иные пары углов, образованные секущими, равными, можно заключать о параллельности или непараллельности прямых. Одна из таких пар — накрест лежащие углы.

Признак параллельности прямых по накрест лежащим углам. Если при пересечении двух прямых секущей накрест лежащие углы равны, то такие прямые параллельны.

Следовательно прямые параллельны. Теорема доказана.

Внешние накрест лежащие углы!

Заметьте, что при доказательстве мы опирались на равенство внутренних накрест лежащих углов, хотя, если взять признак параллельности прямых, тексте теоремы указана общая формулировка — «накрест лежащие углы», без обозначения их расположения относительно полуплоскостей прямых.

Ответ прост: если доказать признаки параллельности прямых, опираясь на равенство внутренних накрест лежащих углов, внешнее расположение — не более чем условность.

Признаки параллельности прямых: задача

Отрезки $AB$ и $CD$ пересекаются в общей середине $O$. Докажите, что прямые $AC$ и $BD$ при этом параллельны.

Признак параллельности прямых

Признак параллельности прямых по соответственным углам. Если при пересечении двух прямых секущей соответственные углы равны, то такие прямые параллельны.

Признак параллельности прямых по сумме односторонних углов. Если при пересечении двух прямых секущей сумма односторонних углов равняется $180^circ$, то такие прямые параллельны.

«Признак» или «теорема»?

Все доказанные признаки параллельности прямых так или иначе в научном понимании является теоремами. При этом, тем не менее, в формулировках слово «теорема» не фигурировало: мы все время пользовались обозначением «признак».

Причина здесь — амбивалентность, создаваемая словосочетанием «теорема параллельности».  Есть аксиома параллельности, а есть, значит, еще и теорема? Тогда аксиома совсем не аксиома, если ей можно противопоставить теорему параллельности. Замена «теорема» на «признак» разрешает данную двойственность.

Параллельные прямые (опорный конспект)

Наглядная геометрия 7 класс. Опорный конспект № 3 Параллельные прямые.

В геометрии нельзя «на глазок» определить, параллельны прямые или нет. Это может быть либо дано, либо доказано. Вы уже знаете, что на плоскости справедлива теорема: «Две прямые, перпендикулярные третьей, параллельны между собой».

Есть еще три признака параллельности прямых, которые можно объединить в одну теорему, она так и называется: «Признаки параллельности прямых». Данные признаки связаны с углами, которые образуются при пересечении двух прямых третьей прямой. Это так называемые накрест лежащие углы, соответственные углы и односторонние углы.

Оказывается, что если накрест лежащие углы равны, или соответственные углы равны, или сумма односторонних углов равна 180°, то прямые будут параллельны.

Справедливы и обратные утверждения. Если даны две заведомо параллельные прямые, которые пересечены третьей, то накрест лежащие углы равны, соответственные углы равны и сумма односторонних углов равна 180°.

Ранее мы доказали, что через точку вне прямой можно провести единственную прямую, перпендикулярную данной. Можно также доказать, что через точку, не лежащую на прямой, можно провести прямую, параллельную данной. А вот доказать, что такая прямая — единственная, нельзя! Утверждение «Через точку, не лежащую на прямой, можно провести ЕДИНСТВЕННУЮ прямую, параллельную данной» называется аксиомой параллельных прямых. У Евклида эта аксиома называлась пятым постулатом.

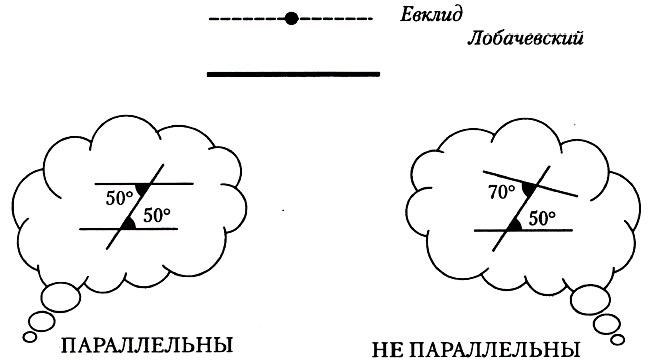
На протяжении двух тысячелетий это утверждение вызывало захватывающие и драматичные споры между такими знаменитыми учеными, как Лобачевский, Гаусс и другие. Споры состояли в том, можно или нельзя доказать этот пятый постулат Евклида на основании уже известных теорем. В конце концов работы в этом направлении привели к полному пересмотру научных представлений о геометрии Вселенной.

При пересечении двух прямых третьей, которая называется секущей, образуется 4 пары накрест лежащих углов, 4 пары соответственных и 4 пары односторонних.

3 и 5; 4 и 6 — внутренние накрест лежащие углы;
1 и 7; 2 и 8 — внешние накрест лежащие углы;
1 и 5; 2 и 6; 4 и 8; 3 и 7 — соответственные углы;
3 и 6; 4 и 5 — внутренние односторонние углы;
2 и 7; 1 и 8 — внешние односторонние углы.

Признаки параллельности прямых. Если накрест лежащие углы равны, ши соответственные углы равны, ши сумма односторонних углов равна 180°, то прямые параллельны. В первую очередь нужно доказать, что если накрест лежащие углы равны, то прямые параллельны. Доказательство опирается на уже доказанное нами свойство: две прямые, перпендикулярные третьей, параллельны между собой. Из середины отрезка секущей опускают перпендикуляр на одну из параллельных прямых. Затем перпендикуляр продляют до пересечения со второй прямой. Из равенства полученных треугольников следует, что прямая, проходящая через перпендикуляр, будет перпендикулярна и второй прямой. Дальнейшее просто.

Через точку, не лежащую на данной прямой, МОЖНО провести прямую, параллельную данной. Опустив перпендикуляр из точки на прямую, а затем, восставив перпендикуляр к проведенной прямой, получим две прямые, перпендикулярные третьей, которые будут параллельны. А вот доказать, что такая прямая единственная, нельзя. Поэтому справедлива АКСИОМА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ: «Через точку, не лежащую на данной прямой, проходит ЕДИНСТВЕННАЯ прямая, параллельная данной».

Теорема о двух прямых, параллельных третьей. Две прямые, параллельные третьей, параллельны между собой. Если бы они пересекались, то через одну точку проходили бы две прямые, параллельные третьей.

Теорема о пересечении параллельных прямых. Если на плоскости прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. Если бы эта прямая не пересекала вторую прямую, то она была бы ей параллельна. Но тогда через одну точку проходили бы две прямые, параллельные третьей. А это невозможно.

Свойства углов при параллельных прямых и секущей. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны, соответственные углы равны и сумма односторонних углов равна 180°. В первую очередь нужно доказать, что если прямые параллельны, то накрест лежащие углы равны. Пусть прямые параллельны, а накрест лежащие углы 1 и 2 не равны. Отложим угол, равный углу 2, как показано на рисунке. Получим еще одну прямую, параллельную нижней прямой (если накрест лежащие углы равны, то прямые параллельны). Но через точку нельзя провести две прямые, параллельные третьей. Значит, наше предположение неверно, и накрест лежащие углы равны. Остальное несложно.

Из указанных свойств параллельных прямых вытекает важное следствие: перпендикуляр к одной из параллельных прямых будет перпендикуляром и к другой. Доказательство следует из равенства соответственных углов.

Теорема об углах с соответственно параллельными сторонами. Углы с соответственно параллельными сторонами равны, если они одновременно острые ши одновременно тупые, и в сумме составляют 180°, если один из них острый, а другой — тупой. Продлив стороны данных углов, получим две пары равных соответственных углов, откуда ∠1 = ∠2. Продлив сторону угла 1 за его вершину, получим доказательство второй части теоремы.

Теорема об углах с соответственно перпендикулярными сторонами. Углы с соответственно перпендикулярными сторонами равны, если они одновременно острые или одновременно тупые, и в сумме составляют 180°, если один из них острый, а другой — тупой. Проведя перпендикулярные лучи из вершины угла 1, получим, что углы 2 и 3 равны и углы 3 и 1 дополняют один и тот же угол 4 до 90°. Значит, ∠1 = ∠3, ∠1 = ∠2. Продлив сторону угла 2 за его вершину, получим доказательство второй части теоремы.

Это опорный конспект № 3 по геометрии в 7 классе «Параллельные прямые (опорный конспект)». Выберите дальнейшие действия:

Решение задач Параллельные прямые. Геометрия 7 класс (УМК Атанасян и др. — Просвещение). Уроки 36-38. Решение задач по теме «Параллельные прямые». Самостоятельные работы с ответами и подсказками к решению.

Геометрия 7. Контрольные работы
   Геометрия 7. Самостоятельные работы

Геометрия 7 класс. Уроки 36-38. Решение задач Параллельные прямые

Основная дидактическая цель урока: совершенствовать навыки решения задач

Задачи с решениями к уроку 36

№ 4. □ ∠ABC = 70°, a ∠BCD = 110°. Могут ли прямые АВ и CD быть: а) параллельными; б) пересекающимися?
Решение:
а) АВ может быть параллельна CD (рис. 3.83, а);
б) АВ и CD могут пересекаться (рис. 3.83, б).

Задачи по готовым чертежам с самопроверкой к уроку 37

I уровень сложности (легкий)

II уровень сложности (средний)

Задачи с самопроверкой к уроку 38

Вы смотрели: Решение задач Параллельные прямые. Геометрия 7 класс (УМК Атанасян и др. — Просвещение). Уроки 36-38. Решение задач по теме «Параллельные прямые». Самостоятельные работы с ответами и решениями. Ориентировано на работу с базовым учебником: «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».

Геометрия 7. Поурочные планы
  Геометрия 7. Самостоятельные работы

Если две паралленльные прямые пересечены секущей, то накрест лежащие углы равны.

Пусть параллельные прямые a и b пересечены секущей c (Рис. 1). Докажем,что

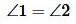
. Предположим, что

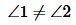
. Отложим от луча MN угол QMN, равной углу 2 так, чтобы углы QMN и 2 были накрест лежащие при пересечении прямых QM и b секущей MN. Поскольку

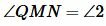
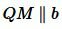
. Получили, что через точку M проходят две прямые, параллельные прямой b, что противоречит аксиоме параллельных прямых (через точку не лежащую на данной прямой проходит только одна прямая, праллельная данной). Следовательно

Пусть прямые a и b параллельны (Рис. 2) и пусть

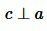
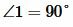
). Прямая a пересекает прямую b (поскольку

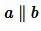
). Но углы 1 и 2 накрест лежащие, следовательно они равы. Т.е.

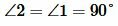
. Следовательно прямые c и b перпендикулярны.

Пусть параллельные прямые a и b пересечены секущей c (Рис.3). Тогда по теореме 1 накрест лежащие углы равны:

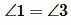
. Углы 2 и 3 вертикальные, т.е.

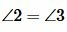
. То есть при пересечении параллельных прямых секущей соответственные углы равны.

Если две паралленльные прямые пересечены секущей, то сумма односторонних углов равна 180°.

Пусть параллельные прямые a и b пересечены секущей c (Рис.3). Покажем, что

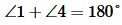
. Накрест лежащие углы равны:

. Углы 3 и 4 смежные. Поэтому

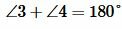
Параллельность прямых (a) и (b) обозначается так:

Teорема 1.  Через две параллельные прямые можно провести плоскость, и притом только одну.

1. так как прямые (a) и (b) параллельны, из определения следует, что через них можно провести плоскость

2. Чтобы доказать, что такая плоскость только одна, на прямой (a) обозначаем точки (B) и (C), а на прямой (b) — точку (A).

3. Так как через три точки, которые не лежат на одной прямой, можно провести только одну плоскость ((2) аксиома), то

является единственной плоскостью, которой принадлежат прямые (a) и (b).

Теорема 2.  Через любую точку пространства вне данной прямой можно провести прямую, параллельную данной прямой, и притом только одну.

1. через данную прямую (a) и точку (M), которая не лежит на прямой, проводится плоскость

2. Такая плоскость только одна (т. к. через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну).

3. А в плоскости

через точку (M) можно провести только одну прямую (b), которая параллельна прямой (a).

Теорема 3.  Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

рассмотрим две параллельные прямые (a) и (b) и допустим, что прямая (b) пересекает плоскость

в точке (M) (1 рис.).

Из (1)-й теоремы известно, что через параллельные прямые (a) и (b) можно провести только одну плоскость

Так как точка (M) находится на прямой (b), то (M) также принадлежит плоскости

(2 рис.). Если у плоскостей

есть общая точка (M), то у этих плоскостей есть общая прямая (c), которая является прямой пересечения этих плоскостей ((4) аксиома).

Прямые (a), (b) и (c) находятся в плоскости

Если в этой плоскости одна из параллельных прямых (b) пересекает прямую (c), то вторая прямая (a) тоже пересекает (c).

Точку пересечения прямых (a) и (c) обозначим за (K).

Так как точка (K) находится на прямой (c), то (K) находится в плоскости

и является единственной общей точкой прямой (a) и плоскости

Значит, прямая (a) пересекает плоскость

в точке (K).

Теорема 4.  Две прямые, параллельные третьей прямой, параллельны.

выберем точку (M) на прямой (b).

Через точку (M) и прямую (a), которая не содержит эту точку, можно провести только одну плоскость

(через прямую и не лежащую на ней точку можно провести только одну плоскость).

Возможны два случая:

1) прямая (b) пересекает плоскость

; или 2) прямая (b) находится в плоскости

Пусть прямая (b) пересекает плоскость

Значит, прямая (c), которая параллельна прямой (b), тоже пересекает плоскость

, то получается, что (a) тоже пересекает эту плоскость. Но прямая (a) не может одновременно пересекать плоскость

и находиться в плоскости

. Получаем противоречие, следовательно,  предположение, что прямая (b) пересекает плоскость

, является неверным.

Значит, прямая (b) находится в плоскости

Теперь нужно доказать, что прямые (a) и (b) параллельны.

Пусть у прямых (a) и (b) есть общая точка (L).

Это означает, что через точку (L) проведены две прямые (a) и (b), которые параллельны прямой (c). Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые (a) и (b) не имеют общих точек.

Так как прямые (a) и (b) находятся в одной плоскости

, и у них нет общих точек, то они параллельны.

Всё множество прямых в пространстве, которые параллельны данной прямой, называется пучком параллельных прямых.

1) любые две прямые пучка параллельных прямых параллельны между собой.

2) Параллельности прямых в пространстве присуща транзитивность:

одна сторона параллелограмма пересекает плоскость. Докажите, что прямая, которая содержит противоположную сторону параллелограмма, тоже пересекает эту плоскость.

Допустим, что у параллелограмма (ABCD) сторона (AD) пересекает плоскость

Так как противоположные стороны параллелограмма параллельны, то, согласно третьей теореме, прямая, которая содержит сторону (BC), тоже пересекает плоскость

2) прямая и плоскость имеют только одну общую точку (прямая и плоскость пересекаются);

3) прямая и плоскость не имеют ни одной общей точки.

Теорема 5 «Признак параллельности прямой и плоскости».Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.

В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.

Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.

Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.

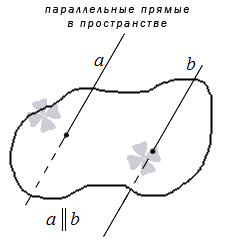
Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.

Чтобы обозначить параллельность прямых, общепринято использовать символ ∥. Т.е., если заданные прямые a и b параллельны, кратко записать это условие нужно так: a ‖ b. Словесно параллельность прямых обозначается следующим образом: прямые a и b параллельны, или прямая а параллельна прямой b, или прямая b параллельна прямой а.

Сформулируем утверждение, играющее важную роль в изучаемой теме.

Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.

В случае, когда речь идет о пространстве, верна теорема:

Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.

Эту теорему просто доказать на базе вышеуказанной аксиомы (программа геометрии 10-11 классов).